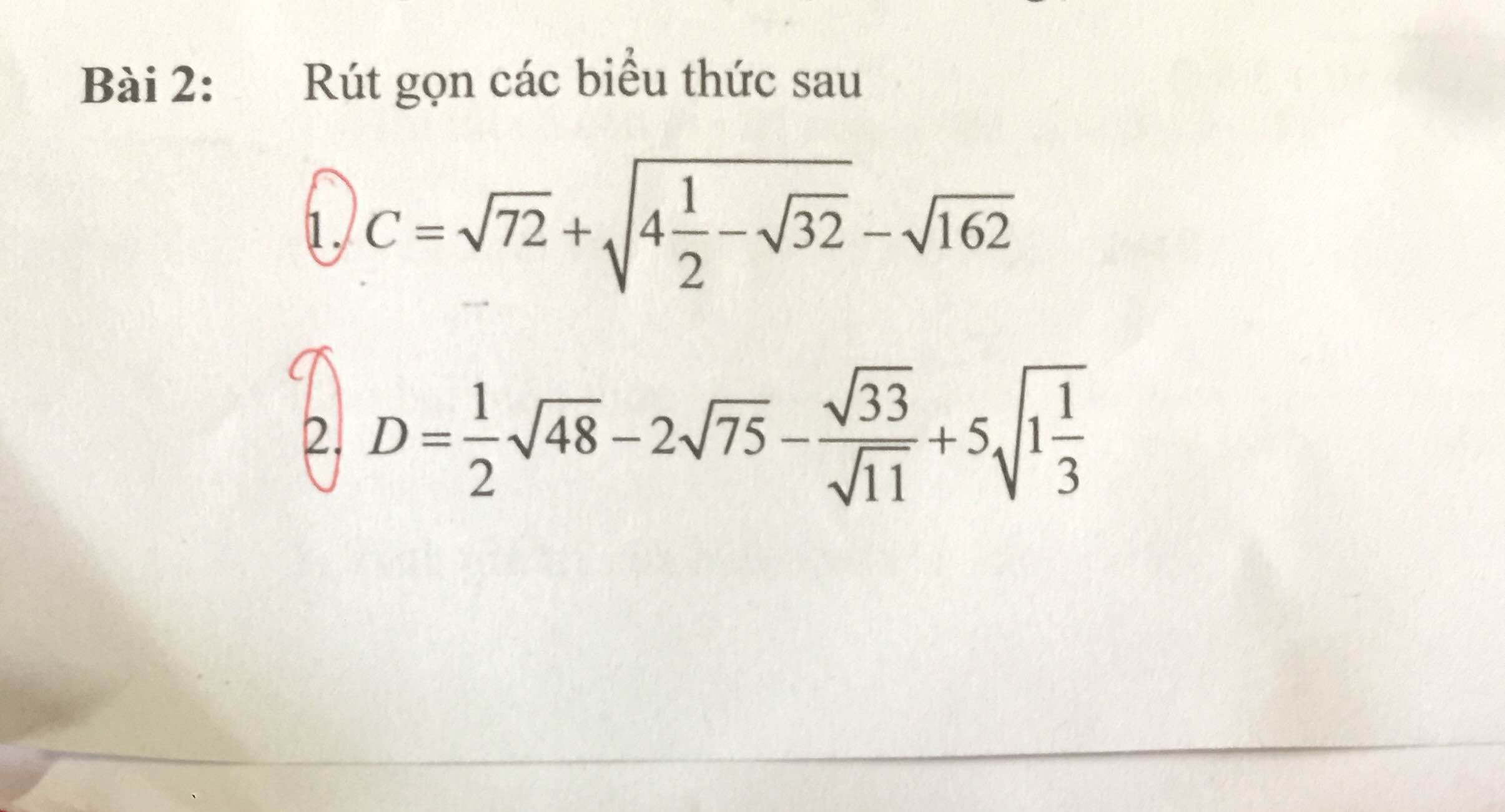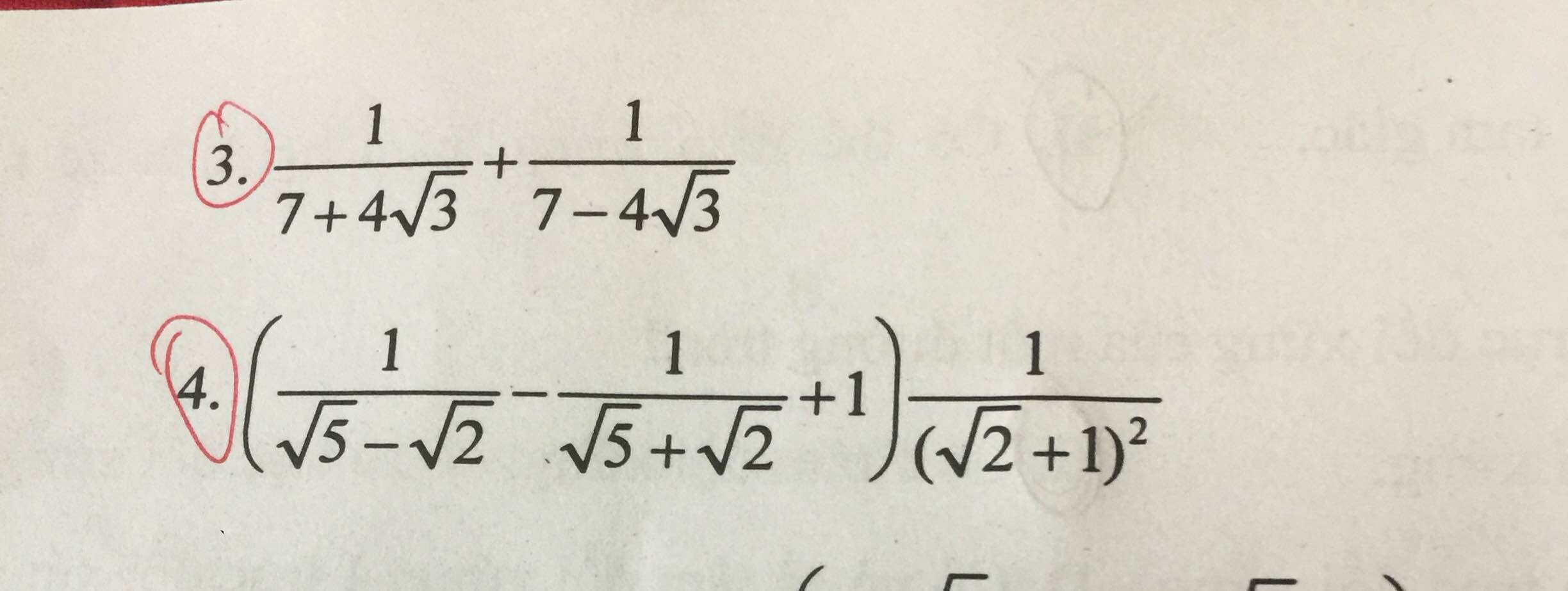Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,C=\left(\dfrac{4\sqrt{x}}{2+\sqrt{x}}+\dfrac{8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1}{x-8\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\left(dk:x>0,x\ne4,x\ne64\right)\)
\(=\left(\dfrac{4\sqrt{x}\left(2-\sqrt{x}\right)+8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1-2\left(\sqrt{x}-8\right)}{\sqrt{x}\left(\sqrt{x}-8\right)}\right)\)
\(=\dfrac{8\sqrt{x}-4x+8x}{4-x}.\dfrac{\sqrt{x}\left(\sqrt{x}-8\right)}{\sqrt{x}-1-2\sqrt{x}+16}\)
\(=\dfrac{8\sqrt{x}+4x}{4-x}.\dfrac{\sqrt{x}\left(\sqrt{x}-8\right)}{-\sqrt{x}+15}\)
\(=\dfrac{4\sqrt{x}\left(2+\sqrt{x}\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-8\right)}{15-\sqrt{x}}\)
\(=\dfrac{4x\left(\sqrt{x}-8\right)}{ \left(2-\sqrt{x}\right)\left(15-\sqrt{x}\right)}\\ =\dfrac{4x\sqrt{x}-32x}{30-2\sqrt{x}-15\sqrt{x}+x}\\ =\dfrac{4x\sqrt{x}-32}{x-17\sqrt{x}+30}\)
\(b,C=-1\Leftrightarrow\dfrac{4x\sqrt{x}-32}{x-17\sqrt{x}+30}=-1\\ \Leftrightarrow4x\sqrt{x}-32+x-17\sqrt{x}+30=0\)
\(\Leftrightarrow4x\sqrt{x}-17\sqrt{x}+x-2=0\\ \Leftrightarrow x=4\left(ktmdk\right)\)
Vậy không có giá trị x thỏa mãn đề bài.

\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

Câu 2:
a: Thay m=-1 vào (1), ta được:
\(x^2-2x+2\cdot\left(-1\right)+3=0\)
=>x=1
b: \(\text{Δ}=\left(2m+4\right)^2-4\left(2m+3\right)=4m^2+16m+16-8m-12\)
\(=4m^2-4m+4=\left(2m-1\right)^2+3>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-1< =0\)
\(\Leftrightarrow\left(2m+4\right)^2-2\left(2m-3\right)-1< =0\)
\(\Leftrightarrow4m^2+16m+16-4m+6-1< =0\)
\(\Leftrightarrow4m^2+12m+21< =0\)
\(\Leftrightarrow m\in\varnothing\)

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm


Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.
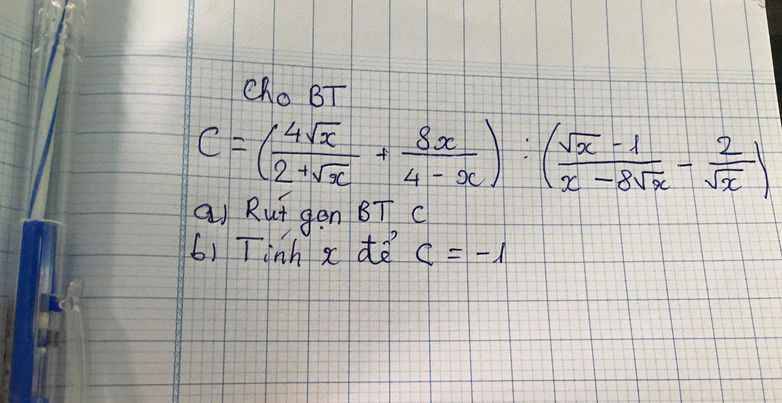

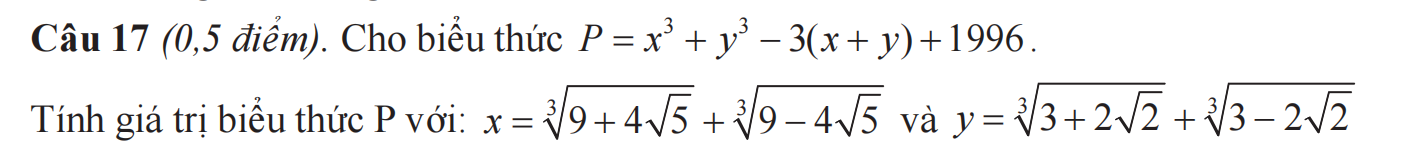 cảm ơn
cảm ơn