
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3x=4z\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\); \(\dfrac{x}{5}=\dfrac{y}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}=\dfrac{x-y+z}{20-24+15}=\dfrac{121}{11}=11\)
\(\Rightarrow x=20.11=220;z=15.11=165;y=264\)

4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI

Bài 7:
a:
Ta có: ΔABC đều
=>AB=AC=BC và \(\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^0\)
Xét ΔABC có \(\widehat{ACE}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACE}=\widehat{CAB}+\widehat{CBA}=120^0\)
Xét ΔACE có \(\widehat{ACE}>90^0\)
nên AE là cạnh lớn nhất trong ΔACE
=>AE>AC
=>AE>AB
b: Xét ΔCAE có CA=CE(=BC)
nên ΔCAE cân tại C
=>\(\widehat{CAE}=\dfrac{180^0-120^0}{2}=30^0\)
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
=>\(\widehat{HAC}=\dfrac{\widehat{BAC}}{2}=30^0\)
=>\(\widehat{HAC}=\widehat{CAE}\)
=>AC là phân giác của góc HAE
bài 9:
a: ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC
b: Xét ΔAHM vuông tại H có AM là cạnh huyền
nên AM là cạnh lớn nhất trong ΔAHM
=>AM>AH
Xét ΔAHM có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{AHM}+\widehat{HAM}=90^0+\widehat{HAM}\)
=>\(\widehat{AMB}>90^0\)
Xét ΔAMB có \(\widehat{AMB}>90^0\)
nên AB là cạnh lớn nhất trong ΔAMB
=>AB>AM
=>AB>AM>AH
=>AC>AM>AH

a) Xét ΔADB và ΔADC có
AB=AC(gt)
AD chung
DB=DC(D là trung điểm của BC)
Do đó: ΔADB=ΔADC(c-c-c)
b) Ta có: AB=AC(gt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DB=DC(D là trung điểm của BC)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của BC
hay AD⊥BC(đpcm)
c) Ta có: CE⊥BC(gt)
AD⊥BC(cmt)
Do đó: EC//AD(Định lí 1 từ vuông góc tới song song)

Bài 4:
Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó:ABCD là hình bình hành
Suy ra: AD//BC
Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE//CB
mà AD//BC
và AE,AD có điểm chung là A
nên E,A,D thẳng hàng

=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

Mình nghĩ :vẽ thêm tia Nx // Tz
Có xNT= NTz (2 góc so le trong) mà NTz=90 độ (GT)
Suy ra xNT=90 độ
Có xNM+xNT=120 độ
Thay số : xNM+90=120
Suy ra xNM+30 độ
Có xNM+NMu=180 độ( vì 30+150 = 180 )
xNM và NMu ở vị trí trong cùng phía nên Mu // Nx
Có Mu//Nx ( Chứng minh trên) điều 1
Nx // Tz ( Vẽ thêm) điều 2
Từ 1 vaf2 suy ra Mu//Tz

ta có các khối: 6,7,8,9 lần lượt tỉ lệ với 3 ; 3,5 ; 4,5 ;4 hay
6/3 = 7/3,5 = 8/4,5 =9/4 = 6+7+8+9 / 3+3,5+4,5+4
=660/15=44
Từ 6/3 =44 => khối 6= 44 * 3 = 132 (h/s)
7/3,5 =44 => khối 7 =44 *3,5 =154 (h/s)
8/4,5 =44 => khối 8 = 44 * 4,5 =198 (h/s)
9/4 = 44 => khối 9 =44 * 4=176 (h/s)
Vậy khối 6 132 h/s
7 154 h/s
8 198 h/s
9 176 h/s
Gọi số học sinh khối 6,7,8,9 là a,b,c,d
Vì số học sinh khối 6,7,8,9 theo thứ tự tỉ lệ với các số 3; 3,5; 4,5; 4
→ Ta có: \(\frac{a}{3}=\frac{b}{3,5}=\frac{c}{4,5}=\frac{d}{4}\)
Và a+b+c+d = 660
Áp dụng tính chất các dãy phân số bằng nhau
\(\Rightarrow\frac{a}{3}=\frac{b}{3,5}=\frac{c}{4,5}=\frac{d}{4}=\frac{a+b+c+d}{3+3,5+4,5+4}=\frac{660}{15}=44\)
\(\Rightarrow\) a = 44.3 = 132 học sinh
b = 44.3,5 = 154 học sinh
c = 44.4,5 = 198 học sinh
d = 44.4 = 176 học sinh
Vậy: Khối 6: 132 học sinh Khối 8: 198 học sinh
Khối 7: 154 học sinh Khối 9: 176 học sinh
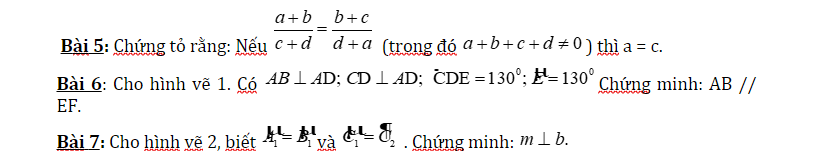





 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn