K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp mình bài 4 và bài 5 với ạ
B
11 tháng 1 2023
`a, 18(x-16)=-36`
`=>x-16=-36:18`
`=>x-16=-2`
`=>x=-2+16`
`=>x= 14`
`b,(-12-x):(-5)=3`
`=>-12-x=3 . (-5)`
`=>-12-x=-15`
`=>x= -12-(-15)`
`=>x=-12+15`
`=>x= 3`
`c,11-(-53+x)=97`
`=>-53+x=11-97`
`=>-53+x=-86`
`=>x=-86-(-53)`
`=>x=-86+53`
`=>x= -33`
`d,-9.x+(-7).x=-48`
`=> [-9+(-7) ].x=-48`
`=>-16.x=-48`
`=>x=-48:(-16)`
`=>x= 3`
`e,(2x-1)^3=-27`
`=> (2x-1)^3=-3^3`
`=> 2x-1=-3`
`=>2x=-3+1`
`=>2x=-2`
`=>x=-2:2`
`=>x=-1`
bn tách ra nhé!
Y
11 tháng 1 2023
Bài 5 :
\(a,5x-16=40+x\)
\(\Leftrightarrow5x-x=40+16\)
\(\Leftrightarrow4x=56\)
\(\Leftrightarrow x=14\)
\(b,-41+2x-\left(-24\right)=4x-23-x\)
\(\Leftrightarrow-41+2x+24=4x-23-x\)
\(\Leftrightarrow2x-4x+x=41-24-23\)
\(\Leftrightarrow-x=-6\)
\(\Leftrightarrow x=6\)
\(c,2\left(x-5\right)-\left(x+6\right)=\left(-7\right)^2\)
\(\Leftrightarrow2x-10-x-6=49\)
\(\Leftrightarrow x=65\)
\(d,120-4\left(1-x\right)=106-3x\)
\(\Leftrightarrow120-4+4x=106-3x\)
\(\Leftrightarrow4x+3x=106-120+4\)
\(\Leftrightarrow7x=-10\)
\(\Leftrightarrow x=-\dfrac{10}{7}\)
13 tháng 1 2023
Bài 4:
Gọi thời gian cần tìm là x
Theo đề, ta có: -6+4x+0+2x=-3+3x
=>6x-6=3x-3
=>3x=3
=>x=1
NP
8
T
22 tháng 10 2023
\(A=1+4+7+...+91+94+95\)
Đặt \(B=1+4+7+...+91+94\)
Số các số hạng của B là:
\((94-1):3+1=32(số)\)
Tổng B bằng:
\((94+1)\cdot 32:2=1520\)
Thay \(B=1520\) vào \(A\), ta được:
\(A=1520+95=1615\)
TL
1
TL
1
21 tháng 4 2023
3:
1: Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có: 6/5a*4/5b=ab-30
=>ab=750
=>S=750
2:
Sau 1,5h thì xe 1 đi được 15*1,5=22,5(km)
Hiệu vận tốc là 20-15=5(km/h)
Thời gian hai xe đuổi kịp nhau là:
22,5/5=4,5(h)
=>Người 1 đi đến B sau 5h
ĐỘ dài AB là:
15*5=75km
TL
2
21 tháng 8
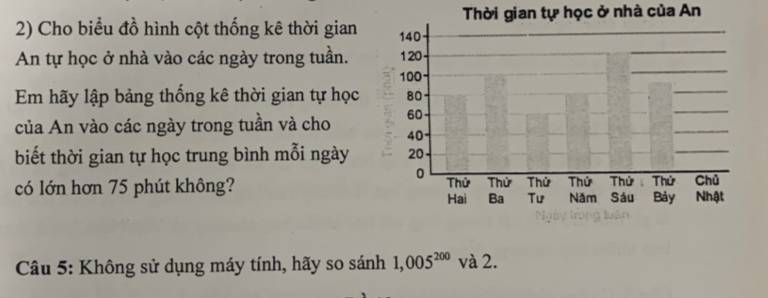
bài 1
| thứ | 2 | 3 | 4 | 5 | 6 | 7 | CN |
| TG học | 80p | 100p | 60p | 80p | 120p | 90p | 0p |
TBC TG bạn học 1 ngày là : (80*2+100+60+120+90+0)/7 \(\approx\) 76
Vậy TG bạn học 1 ngày là hơn 75p
2
ko bt nhưng chắc chắn là 1,005200
LỚN HƠN NHA
TL
1
4a.
$A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+....+\frac{1}{2^{100}}$
$2A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{99}}$
$\Rightarrow 2A-A=(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{99}})-(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+....+\frac{1}{2^{100}})$
$\Rightarrow A=1-\frac{1}{2^{100}}$
4b.
$B=1+\frac{1}{3}+\frac{1}{3^2}+....+\frac{1}{3^{100}}$
$3B=3+1+\frac{1}{3}+...+\frac{1}{3^{99}}$
$\Rightarrow 3B-B=(3+1+\frac{1}{3}+...+\frac{1}{3^{99}})-(1+\frac{1}{3}+\frac{1}{3^2}+....+\frac{1}{3^{100}})$
$\Rightarrow 2B=3-\frac{1}{3^{100}}$
$\Rightarrow B=\frac{3}{2}-\frac{1}{2.3^{100}}$