
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

Ta có: DE//AC (cùng vuông góc với AB)
Áp dụng định lý Ta-lét ta có:
\(\dfrac{BD}{AD}=\dfrac{BE}{CE}\Rightarrow\dfrac{BD}{AD}=\dfrac{BE}{BC-BE}\Rightarrow\dfrac{6}{x}=\dfrac{3x}{13,5-3x}\)
\(\Leftrightarrow6\left(13,5-3x\right)=x\cdot3x\)
\(\Leftrightarrow81-18x=3x^2\)
\(\Leftrightarrow27-6x=x^2\)
\(\Leftrightarrow x^2+6x-27=0\)
\(\Leftrightarrow x^2-3x+9x-27=0\)
\(\Leftrightarrow x\left(x-3\right)+9\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-9\left(ktm\right)\end{matrix}\right.\)
Vậy: `x=3`

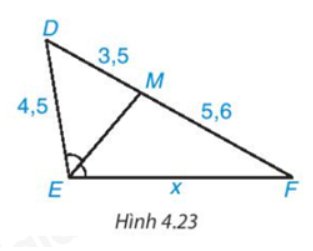
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

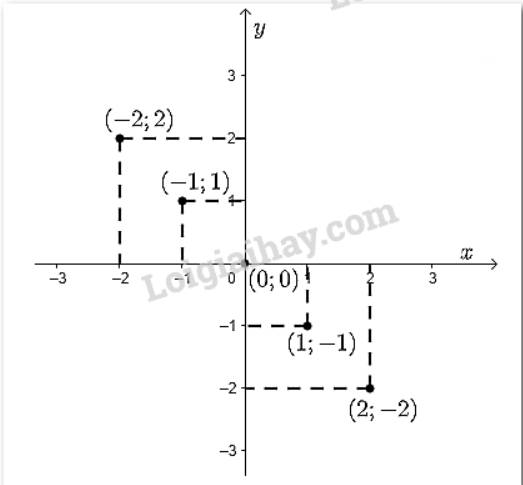
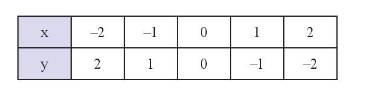
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:

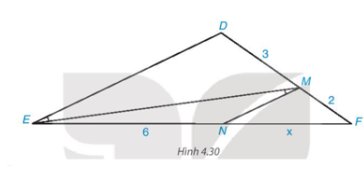
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

a) Dùng 
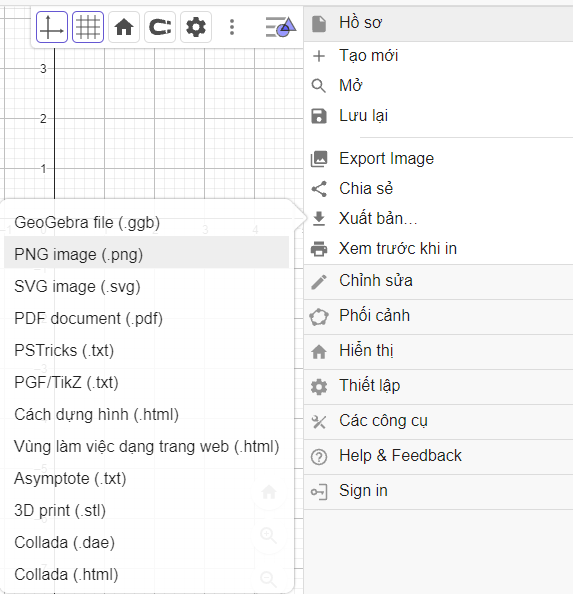
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
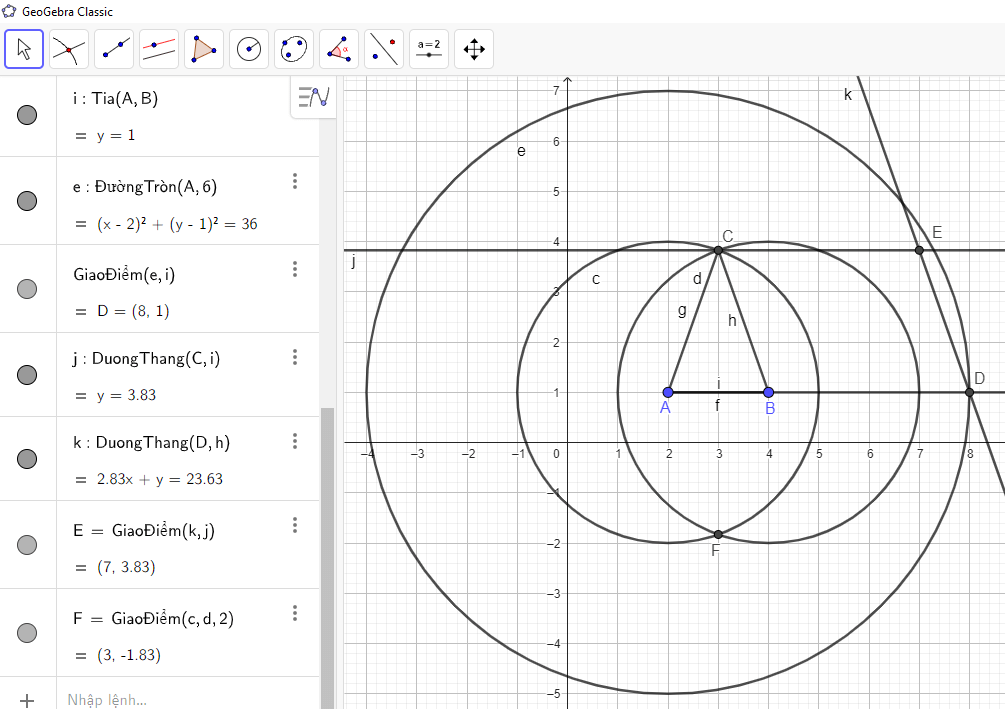
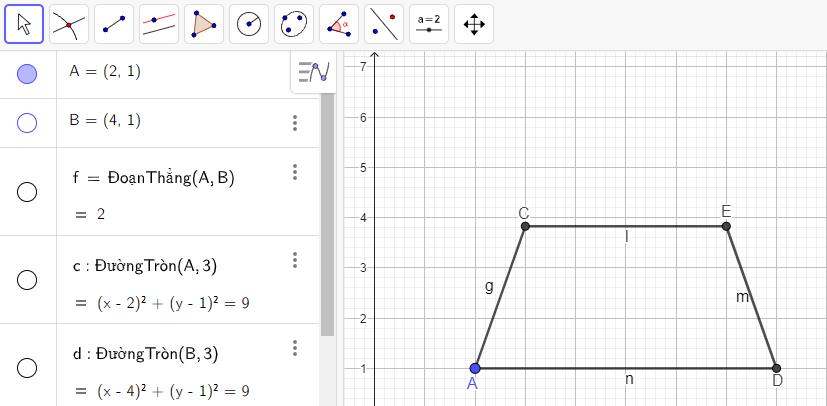
c) Vẽ hình thang cân ADEC có AD // EC, AD = 6 cm, CE = 4 cm, AC = DE = 3 cm theo các bước sau:
Bước 1. Vẽ đoạn thẳng AB và có độ dài bằng AD – EC = 2 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ tam giác ABC có BC = 3 cm (độ dài của DE), AC = 3 cm.
Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Bước 4. Vẽ điểm E sao cho DE // BC và CE // AB.
Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Ẩn các đường tròn, các đường thẳng, đoạn thẳng AB, BC và điểm B. Chọn công cụ 










 trong công cụ
trong công cụ  để kiểm tra DE có bằng 4 cm không.
để kiểm tra DE có bằng 4 cm không.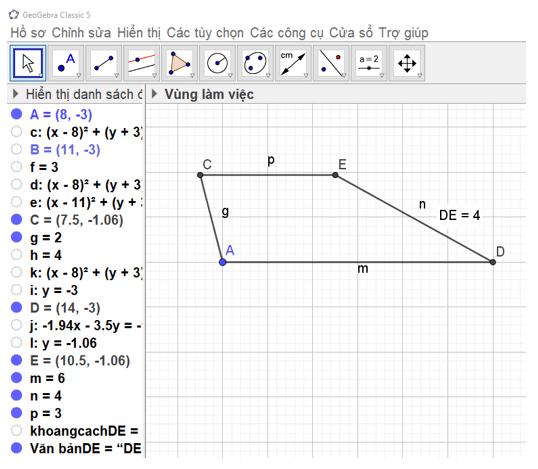
3:
Số tiền phải trả trước khi giảm giá lần 2 là:
15390000:95%=16200000(đồng)
Số tiền vốn là:
16200000:90%=18000000(đồng)