
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mk nghĩ là nếu nhún thì sẽ có đà nhảy lên nhưng mà k nhún vẫn có thể nhảy lên mà =)) haha
ht
ht
ht
ht
ht
TL:
Nếu không nhún chân khi nhảy lên thì sẽ không có lực để có thể nhảy lên
Mik ko chắc nha
@@@@@@
HT

Dụng cụ thí nghiệm:
- Cái thước đo chiều cao: Để đo khoảng cách từ điểm thả đến mặt đất.
- Thời gian đo: Một chiếc đồng hồ bấm giây hoặc thiết bị đo thời gian chính xác.
- Vật thể rơi: Một vật thể có khối lượng nhỏ (như quả bóng, viên bi) để thả.
- Giá đỡ: Để giữ thước đo chiều cao hoặc hỗ trợ cho việc thả vật thể.
- Bảng ghi kết quả: Để ghi lại thời gian và các thông số khác trong quá trình thí nghiệm Cô xem đúng không ạ
* Dụng cụ thí nghiệm:
- Máng đứng, có gắn dây rọi (1)
- Vật bằng thép hình trụ (2)
- Nam châm điện N (3), dùng giữ và thả trụ thép
- Cổng quang điện E (4)
- Giá đỡ có đế ba chân, có vít chỉnh cân bằng và trụ thép (5)
- Đồng hồ đo thời gian hiện số (6)
- Công tắc kép (7)
* Các bước tiến hành thí nghiệm:
1. Cắm nam châm điện vào ổ A và cổng quang vào ổ B ở mặt sau của đồng hồ đo thời gian hiện số.
2. Đặt MODE đồng hồ đo thời gian hiện số ở chế độ thích hợp.
3. Đặt trụ thép tại vị trí tiếp cúc với nam châm điện N và bị giữ lại ở đó.
4. Nhấn nút RESET của đồng hồ để chuyến các số hiển thị về giá trị ban đầu 0.000.
5. Nhấn nút của hộp công tắc kép để ngắt điện vào nam châm điện: trụ thép rơi xuống và chuyển động đi qua cổng quang điện.
6. Ghi lại các giá trị thời gian hiển thị trên đồng hồ.
7. Dịch chuyển cổng quang điện ra xa dần nam châm điện, thực hiện lại các thao tác 3, 4, 5, 6 bốn lần nữa. Ghi các giá trị thời gian t tương ứng với quãng đường s.

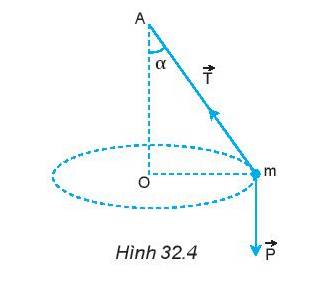
Hợp lực của lực căng dây \(\overrightarrow T \)và trọng lực \(\overrightarrow P \):
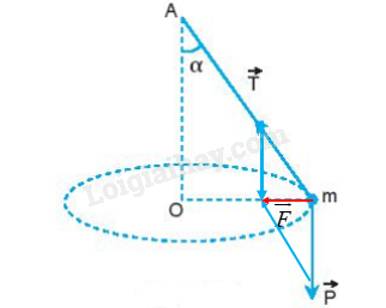
Lực hướng tâm chính là hợp lực của \(\overrightarrow T \)và \(\overrightarrow P \).



1.47
Tóm tắt ; a=g=10m/s^2( gia tốc của rơi tự do là g=9,81m/s^2 nhưng mk lấy là 10m/s^2 cho tròn số )
t1=5s
t2=3s
a) S1(chiều dài giêngs)=?
b)V=? (vận tốc của vật khi chạm đất )
c)S2(quảng đường vật rơi sau 3s)=?
Giải
a) S1=1/2.g.t1^2=1/2.10.5^2=125(m)
b)V=at=10.5=50(m/s)
c) S2=1/2.g.t2^2=1/2.10.3^2=45(m)
1.47
a) h = 1/2 gt2= 1/2.10.52= 125m
b) v= gt = 10.5 = 50m/s
c) quãng đường vật rơi trong 3s:
s1= 1/2gt2 = 1/2.10.32= 45m
quãng đường vật rơi trong 2s:
s2= 1/2gt2= 1/2.10.22= 20m
quãng đường vật rơi trong giây thứ 3 là:
s = s1 - s2 = 45 - 20 = 25m













Câu 18.7.
Chọn hệ trục tọa độ Oxxy như hình.
Áp dụng định luật II Niuton ta có: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
\(Oy:N-Pcos\alpha-Fsin\alpha=0\) \(\Rightarrow N=Pcos\alpha+Fsin\alpha\)
Có \(F_{ms}=k\cdot N=k\cdot\left(Pcos\alpha+Fsin\alpha\right)=k\cdot\left(mgcos\alpha+Fsin\alpha\right)\)
\(Ox:Psin\alpha-Fcos\alpha-F_{ms}=0\)
\(\Rightarrow Fcos\alpha=Psin\alpha-F_{ms}=mgsin\alpha-k\left(mgcos\alpha+Fsin\alpha\right)\)
\(\Rightarrow F\left(cos\alpha+k.sin\alpha\right)=mg\left(sin\alpha-kcos\alpha\right)\)
\(\Rightarrow\left\{{}\begin{matrix}F_{min}=\dfrac{mg\left(sin\alpha-kcos\alpha\right)}{cos\alpha+ksin\alpha}=\dfrac{mg\left(tg\alpha-k\right)}{1+k.tg\alpha}\\F_{max}=\dfrac{mg\left(tg\alpha+k\right)}{1-k.tg\alpha}\end{matrix}\right.\)
Câu 18.8.
Chọn hệ trục tọa độ Oxy như hình vẽ.
Áp dụng định luật II Niuton: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=\overrightarrow{0}\) \(\left(1\right)\)
\(Ox:Fcos\beta-Psin\alpha-F_{ms}=0\Rightarrow F_{ms}=Psin\alpha-Fcos\beta\)
\(Oy:N+Fsin\beta-Pcos\alpha=0\Rightarrow N=Pcos\alpha-Fsin\beta\)
Thay lần lượt vào \(\left(1\right)\) ta được:
\(F+P+Pcos\alpha-Fsin\beta+Psin\alpha-Fcos\beta=0\)
\(\Rightarrow F\left(cos\beta+sin\beta\right)=P\left(cos\alpha+sin\alpha\right)\)
Để \(F_{min}\Leftrightarrow\left(cos\beta+sin\beta\right)_{max}=tan\beta\)
\(\Rightarrow\beta=arctan\left(cos\beta+sin\beta\right)\)
Đặt \(cos\beta+sin\beta=k\)
Khi đó: \(\beta=arctank=arctgk\)