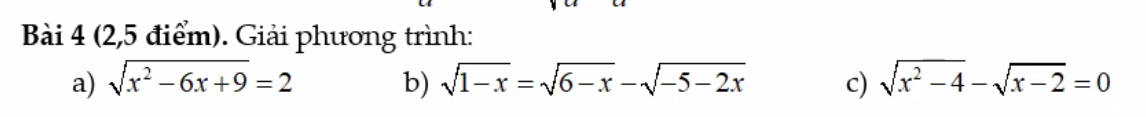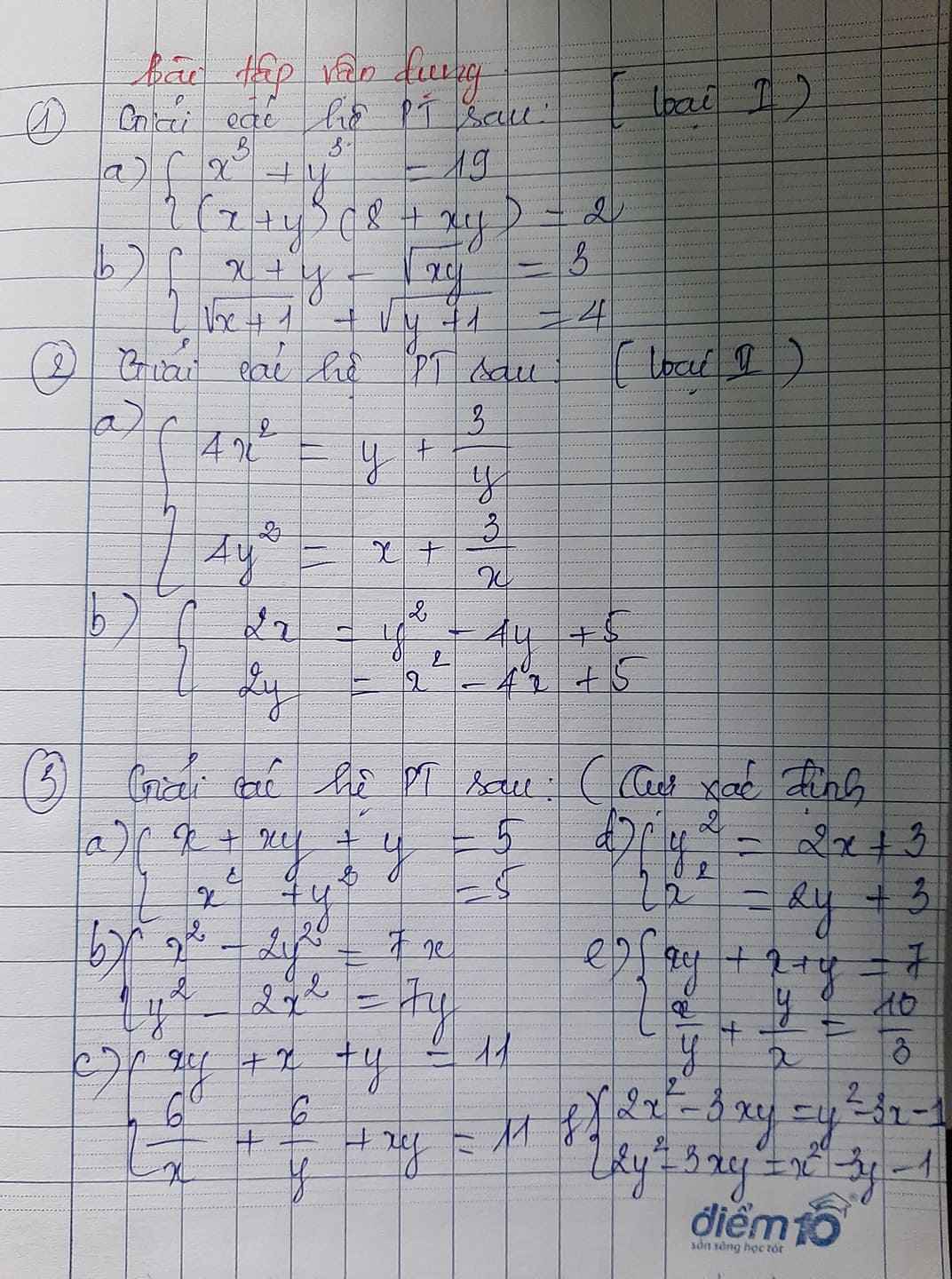K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
3 tháng 9 2021
a, \(\sqrt{x^2-6x+9}=2\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=2\)
\(\Leftrightarrow\left|x-3\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=2\\x-3=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
3 tháng 9 2021
a: Ta có: \(\sqrt{x^2-6x+9}=2\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
24 tháng 10 2021
Bài 1:
1:
a: \(\sqrt{12}+3\sqrt{48}-5\sqrt{75}\)
\(=2\sqrt{3}+12\sqrt{3}-25\sqrt{3}\)
\(=-11\sqrt{3}\)
HT
1 tháng 8 2021
2.
a)\(\left\{{}\begin{matrix}4x^2=y+\dfrac{3}{y}\\4y^2=x+\dfrac{3}{x}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x^2:\dfrac{1}{y}=\left(y+\dfrac{3}{y}\right):\dfrac{1}{y}\\4y^2:\dfrac{1}{x}=\left(x+\dfrac{3}{x}\right):\dfrac{1}{x}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x^2y=y^2+3\left(1\right)\\4y^2x=x^2+3\left(2\right)\end{matrix}\right.\) (1)-(2)<=>4x2y-4y2x=y2-x2
<=>4xy(x-y)=-(x-y)(x+y)<=>4xy(x-y)+(x-y)(x+y)=0
<=>(x-y)(x+y+4xy)=0<=>\(\left\{{}\begin{matrix}x-y=0=>x=y\\x+y+4xy=0=>x=\dfrac{-y}{1+4y}\end{matrix}\right.\)
Tới đó xét từng th rồi thế vô tìm x, y nha bạn.
HT
1 tháng 8 2021
b)\(\left\{{}\begin{matrix}2x=y^2-4y+5\left(1\right)\\2y=x^2-4x+5\left(2\right)\end{matrix}\right.\) (1)-(2)<=> 2x-2y=y2-x2-4y+4x
<=>(y-x)(y+x)+2(x-y)=0<=>(y-x)(y+x+2)=0
<=>\(\left\{{}\begin{matrix}x=y\\x=-2-y\end{matrix}\right.\)
29 tháng 8 2021
a: Ta có: \(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\)
\(\Leftrightarrow\left|x-2\right|=\left|2x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-2\\2x-3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
29 tháng 8 2021
c: Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-3\\2x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)
PL
2
25 tháng 2 2022
Câu 2.2
để 2 đt song song khi \(\left\{{}\begin{matrix}m^2-1=3\\m+1\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m\ne2\end{matrix}\right.\Leftrightarrow m=2\)
25 tháng 2 2022
Câu 2:
1: \(A=\left(\sqrt{x}+\sqrt{y}-\sqrt{x}+\sqrt{y}-y\right)\cdot\left(\sqrt{y}-2\right)\)
\(=\left(2\sqrt{y}-y\right)\left(\sqrt{y}-2\right)=-\sqrt{y}\left(y-4\sqrt{y}+4\right)=-y\sqrt{y}+4y-4\sqrt{y}\)
TM
1 tháng 9 2023
(a) Phương trình đường thẳng \(\left(d\right)\) có dạng tổng quát: \(y=ax+b\).
Do \(\left(d\right)\) đi qua \(A,B\) nên giá trị hoành độ và tung độ của \(A,B\) là các cặp nghiệm của phương trình đường thẳng.
\(\Rightarrow\left\{{}\begin{matrix}-3=a+b\\1=2a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=-7\end{matrix}\right.\).
Vậy: Phương trình đường thẳng \(\left(d\right):y=4x-7\).
(b) Mình không hiểu rõ đề phần "có (1, 2)" ạ:D.
BH
2
28 tháng 7 2020
80)
a)
\(\left(2-\sqrt{2}\right)\left(-5\sqrt{2}\right)-\left(3\sqrt{2}-5\right)^2\)
\(=-10\sqrt{2}+5.2-\left(18-30\sqrt{2}+25\right)\)
Đáp số : \(-33+20\sqrt{2}\)
b)
\(2\sqrt{3a}-\sqrt{75a}+a\sqrt{\frac{13,5}{2a}}-\frac{2}{5}\sqrt{300a^3}\)
\(=2\sqrt{3a}-5\sqrt{3a}+\frac{a}{2a}\sqrt{27a}-\frac{2}{5}.10a\sqrt{3a}\)
Đáp số : \(-\left(1,5+4a\right)\sqrt{3a}\)
28 tháng 7 2020
81)
a) Ta có : \(\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\left(\sqrt{a}+\sqrt{b}\right)^2+\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{a+2\sqrt{ab}+b+a-2\sqrt{ab}+b}{a-b}\)
\(=\frac{2\left(a+b\right)}{a-b}\)( Với \(a\ge0\); \(b\ge0\)và \(a\ne b\))
b) Ta có : \(\frac{a-b}{\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a^3}-\sqrt{b^3}}{a-b}=\frac{\left(a-b\right)\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}\right)^2+\left(\sqrt{b}\right)^2}-\frac{a\sqrt{a}-b\sqrt{b}}{a-b}\)
\(=\frac{a\sqrt{a}+a\sqrt{b}-b\sqrt{a}-b\sqrt{b}}{a-b}-\frac{a\sqrt{a}-b\sqrt{b}}{a-b}\)
\(=\frac{a\sqrt{b}-b\sqrt{a}}{a-b}\)( Với \(a\ge b\); \(b\ge0\)và \(a\ne b\))