
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1 : a . \(lim\dfrac{9n^2-3n-1}{7n^3+3n^2}=lim\dfrac{\dfrac{9}{n}-\dfrac{3}{n^2}-\dfrac{1}{n^3}}{7+\dfrac{3}{n}}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{4x+1}-3}{4-x^2}=lim_{x\rightarrow2}\dfrac{4x+1-9}{\left(\sqrt{4x+1}+3\right)\left(4-x^2\right)}\)
\(=lim_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(\sqrt{4x+1}+3\right)\left(2-x\right)\left(2+x\right)}\)
\(=lim_{x\rightarrow2}\dfrac{-4}{\left(\sqrt{4x+1}+3\right)\left(2+x\right)}=\dfrac{-4}{\left(3+3\right)\left(2+2\right)}=-\dfrac{1}{6}\)
Câu 2 : Ta có : f(x) = \(\left\{{}\begin{matrix}2x^2+x\left(x< 2\right)\\mx-1\left(x\ge2\right)\end{matrix}\right.\)
TXĐ : D = R . Với x < 2 ; hàm số liên tục
Với x > 2 ; hàm số liên tục
Với x = 2 , ta có : \(lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^-}2x^2+x=2.2^2+2=10\)
\(lim_{x\rightarrow2^+}f\left(x\right)=lim_{x\rightarrow2^+}mx-1=2m-1\)
Hàm số liên tục trên R <=> Hàm số liên tục tại x = 2
\(\Leftrightarrow lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^+}f\left(x\right)\)
\(\Leftrightarrow10=2m-1\) \(\Leftrightarrow m=\dfrac{11}{2}\)
Vậy ...

c: \(\left(x^2+x-3\right)'=2x+1\)
(2x-1)'=2
\(y'=\dfrac{\left(2x+1\right)\cdot\left(2x-1\right)-\left(x^2+x-3\right)\cdot2}{\left(2x-1\right)^2}\)
\(=\dfrac{4x^2-1-2x^2-2x+6}{\left(2x-1\right)^2}=\dfrac{2x^2-2x+5}{\left(2x-1\right)^2}\)

8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)

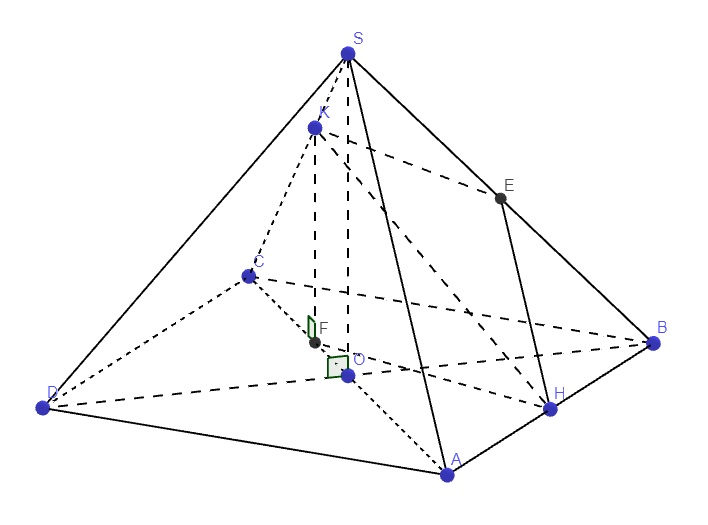
Trong mp đáy, qua B kẻ đường thẳng song song AC, lần lượt cắt DA và DC kéo dài tại E và F
\(\Rightarrow AC||\left(SEF\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SEF\right)\right)=d\left(A;\left(SEF\right)\right)\)
Gọi I là giao điểm AC và BD
Theo định lý Talet: \(\dfrac{ID}{IB}=\dfrac{DC}{AB}=3\Rightarrow\dfrac{ID}{BD}=\dfrac{3}{4}\)
Cũng theo Talet: \(\dfrac{DA}{DE}=\dfrac{DI}{DB}=\dfrac{3}{4}\Rightarrow AD=\dfrac{3}{4}DE\Rightarrow AE=\dfrac{1}{4}DE\)
\(\Rightarrow d\left(A;\left(SEF\right)\right)=\dfrac{1}{4}d\left(D;\left(SEF\right)\right)\)
Trong tam giác vuông EDF, kẻ \(DH\perp EF\) , trong tam giác vuông SDH, kẻ \(DK\perp SH\)
\(\Rightarrow DK\perp\left(SEF\right)\Rightarrow DK=d\left(D;\left(SEF\right)\right)\)
\(DE=\dfrac{4}{3}AD=\dfrac{4a}{3}\); \(DF=\dfrac{4}{3}DC=4a\)
\(\dfrac{1}{DH^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}=\dfrac{5}{8a^2}\)
\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{DH^2}=\dfrac{1}{48a^2}+\dfrac{5}{8a^2}\Rightarrow DK=\dfrac{4a\sqrt{93}}{31}\)
\(\Rightarrow d\left(AC;SB\right)=\dfrac{1}{4}DK=\dfrac{a\sqrt{93}}{31}\)


\(\Leftrightarrow\left(2sinx-1\right)\left(2cos2x+2sinx+3\right)-\left(2sinx-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(2cos2x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\cos2x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)

a.
\(O=AC\cap BD\Rightarrow O\in BD\in\left(SBD\right)\) \(\Rightarrow SO\in\left(SBD\right)\)
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\Rightarrow AC\perp SD\)
b.
O là trung điểm AC, H là trung điểm AB \(\Rightarrow\) OH là đường trung bình tam giác ABC
\(\Rightarrow OH||BC\Rightarrow OH\perp AB\Rightarrow OH\perp CD\) (1)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SHO\right)\)
c.
Theo cmt trên \(OH||BC\Rightarrow OH||AD\)
\(\Rightarrow\widehat{\left(OH;SD\right)}=\widehat{\left(AD;SD\right)}=\widehat{SDA}\)
\(AC=2a\sqrt{2}\Rightarrow OA=a\sqrt{2}\Rightarrow SA=SB=SC=SD=\sqrt{SO^2+OA^2}=a\sqrt{3}\)
Áp dụng định lý hàm cosin trong tam giác SAD:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\widehat{SDA}=...\)
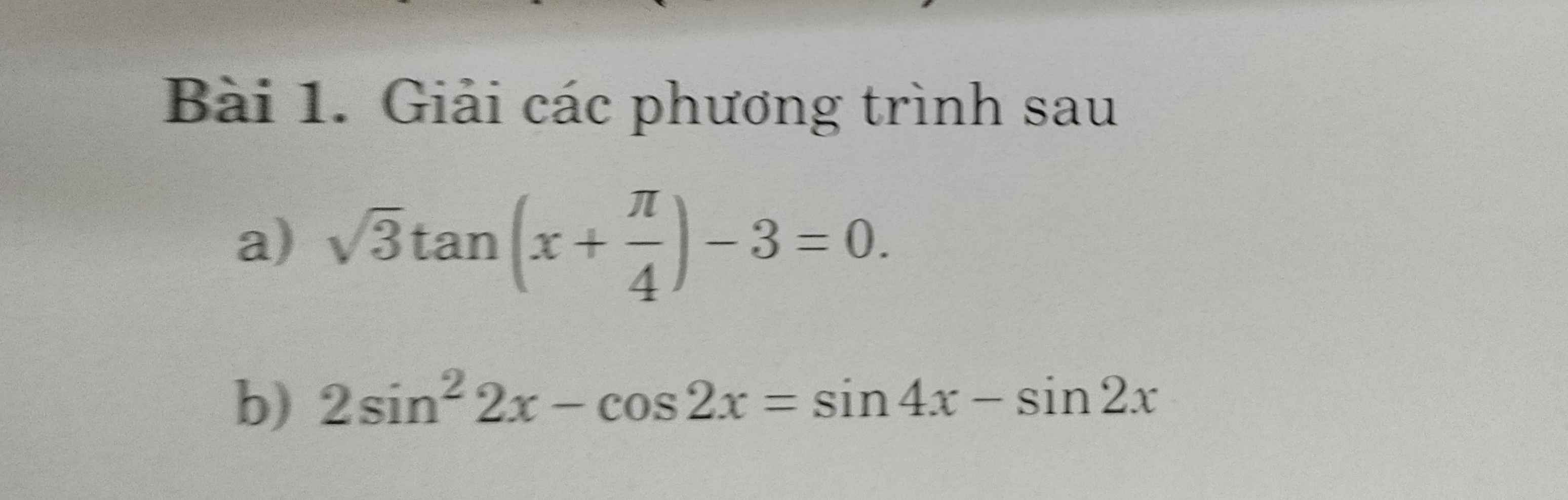
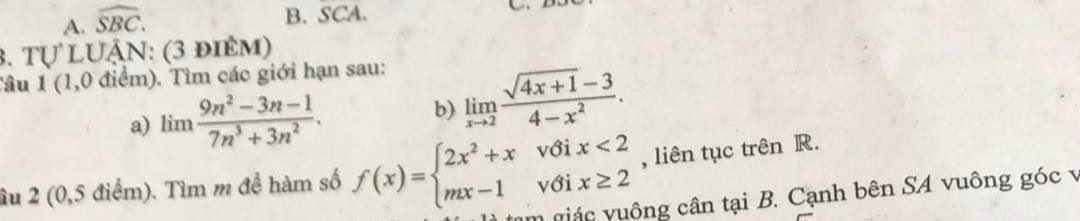
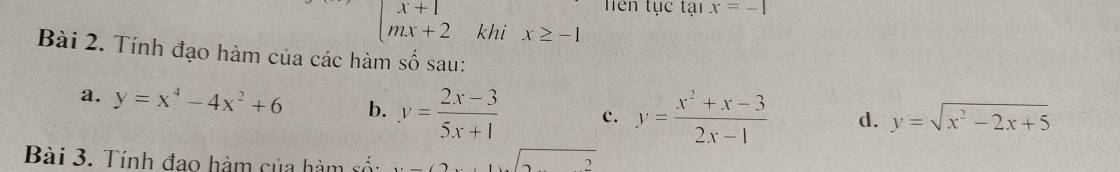




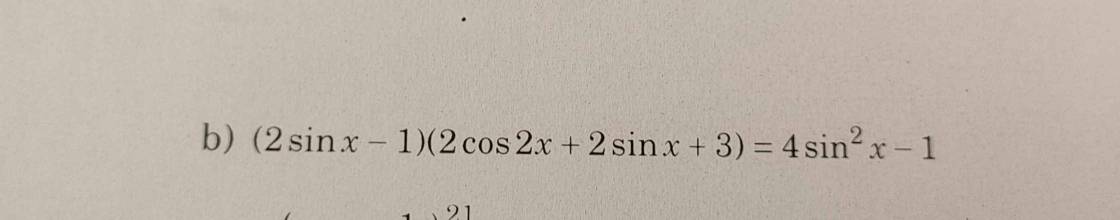

Lời giải:
$2\sin ^22x-\cos 2x=\sin 4x-\sin 2x$
$\Leftrightarrow 2\sin^22x-\cos 2x=2\sin 2x\cos 2x-\sin 2x$
$\Leftrightarrow (2\sin ^22x+\sin 2x)-(\cos 2x+2\sin 2x\cos 2x)=0$
$\Leftrightarrow \sin 2x(2\sin 2x+1)-\cos 2x(1+2\sin 2x)=0$
$\Leftrightarrow (2\sin 2x+1)(\sin 2x-cos 2x)=0$
$\Rightarrow \sin 2x=\frac{-1}{2}$ hoặc $\sin 2x=\cos 2x$
$\Rightarrow \sin 2x=\frac{-1}{2}$ hoặc $\sin 2x=\sin (\frac{\pi}{2}-2x)$
Đến đây thì đơn giản rồi.