Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





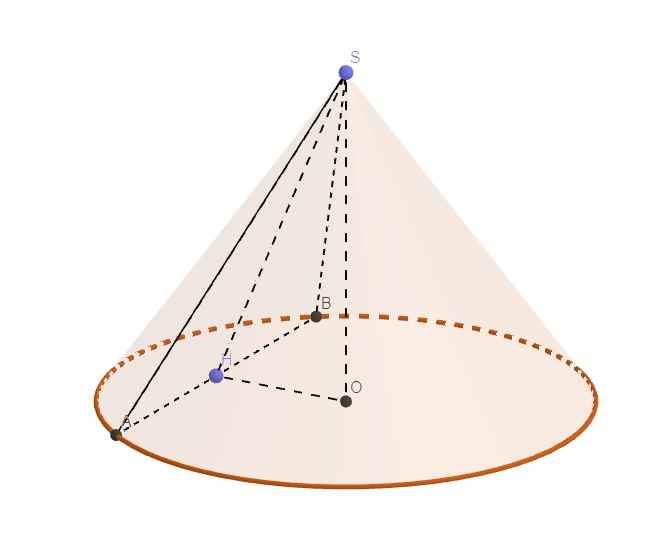
Đặt tên các điểm như hình vẽ, với H là trung điểm AB
\(\Rightarrow\widehat{SHO}=60^0\) (là góc giữa thiết diện và đáy nón)
Tam giác SAB đều \(\Rightarrow SH=\dfrac{AB\sqrt{3}}{2}=2\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow\left\{{}\begin{matrix}OH=SH.cos60^0=\sqrt{3}\\h=SO=SH.sin60^0=3\end{matrix}\right.\)
\(R=OA=\sqrt{AH^2+OH^2}=\sqrt{2^2+3}=\sqrt{7}\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi.7.3=7\pi\left(cm^3\right)\)

Phương trình mặt phẳng (P) qua A và vuông góc \(\overrightarrow{a}\) có dạng:
\(4\left(x-1\right)+2\left(y-1\right)-1\left(z+2\right)=0\)
\(\Leftrightarrow4x+2y-z-8=0\)
Gọi B là giao điểm (P) và \(\Delta\Rightarrow\) tọa độ B thỏa mãn:
\(4\left(2-t\right)+2\left(3+2t\right)-\left(1+3t\right)-8=0\) \(\Rightarrow t=\dfrac{5}{3}\) \(\Rightarrow B\left(\dfrac{1}{3};\dfrac{19}{3};6\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-\dfrac{2}{3};\dfrac{16}{3};8\right)=\dfrac{2}{3}\left(-1;8;12\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=1-t\\y=1+8t\\z=-2+12t\end{matrix}\right.\)

Mặt cầu tâm \(I\left(1;1;0\right)\) bán kính \(R=5\)
\(\Rightarrow IA=\sqrt{6^2+8^2}=10=2R\)
Gọi C là trung điểm IA \(\Rightarrow C\left(4;5;0\right)\Rightarrow IC=R=5\Rightarrow C\in\left(S\right)\)
Gọi D là trung điểm IC \(\Rightarrow D\left(\dfrac{5}{2};3;0\right)\), đồng thời do D là trung điểm IC \(\Rightarrow MD\perp IC\) và IM=IC=R hay tam giác MDF vuông tại D
Lại có: \(CM=CA=CI=R\Rightarrow\) tam giác AMI vuông tại M
\(\Rightarrow\Delta_VMID\sim\Delta_VAIM\) (chung góc I)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{AI}{AM}=\dfrac{2R}{R}=2\Rightarrow MA=2MD\)
\(\Rightarrow P=MA+2MB=2MD+2MB=2\left(MD+MB\right)\ge2DB=2\sqrt{\left(\dfrac{5}{2}\right)^2+\left(3-8\right)^2+0^2}=5\sqrt{5}\)

27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)