Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có : ( 2a2 - a - 7 ) / ( a-2) = \(\frac{2a^2-a-7}{a-2}\)
= \(\frac{\left(2a+3\right)\left(a-2\right)}{\left(a-2\right)}+\frac{\left(-1\right)}{\left(a-2\right)}\)
= 2a + 3 + \(\frac{\left(-1\right)}{ \left(a-2\right)}\)
Để biểu thức trên chia hết cho ( a - 2 ) thì ( -1) phải chia hết cho ( a-2)
=> ( a - 2 ) thuộc Ư(-1) = \(\left\{-1;1\right\}\)
- a - 2 = -1 => a = 1
- a - 2 = 1 => a = 3
Vậy a=1 hoặc a=3 thì 2a2 - a - 7 chia hết cho a-2
hihi
Và các bạn làm cho mình cả những bài mà mình đã gửi lên nữa nhé ! Thanks 
a) \(a^4+4\)
\(=a^4+4a^2+4-4a^2\)
\(=\left(a^2+2\right)^2+\left(2a\right)^2\)
\(=\left(a^2+2a+2\right)\left(a^2-2a+2\right)\)
b) \(\left(x+y+z\right)^3-x^3-y^3-z^3\)
\(=\left[\left(x+y\right)+z\right]^3-x^3-y^3-z^3\)
\(=\left(x+y\right)^3+z^3+3z\left(x+y\right)\left(x+y+z\right)-x^3-y^3-z^3\)
\(=x^3+y^3+3xy\left(x+y\right)+z^3+3z\left(x+y\right)\left(x+y+z\right)-x^3-y^3-z^3\)
\(=3\left(x+y\right)\left(xy+xz+yz+z^2\right)\)
\(=3\left(x+y\right)\left[x\left(y+z\right)+z\left(y+z\right)\right]\)
\(=3\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
Hãy giúp mình với các bạn ơi mình cần gấp lắm
Cảm ơn trước nhé
/hoi-dap/question/66547.html
mình quên chưa đăng câu hỏi sorry nhé
A B C D M E F G H N P Q I K
Gọi EFGH là tứ giác nội tiếp hình vuông
(\(E\in AB,F\in BC,G\in CD,H\in AD\)) , Từ E,F,G,H lần lượt dựng các đường thẳng vuông góc với BD tại P,Q,M,N; I và K là giao điểm của AG và EF.
Ta có : \(AI\ge AM=MP;GI\ge MP=GM;EK\ge EP=BP;KF\ge FQ=BK\)
\(\Rightarrow AG+EF=AI+IG+EK+KF\ge\left(PM+BQ\right)+\left(PN+BP\right)\)
Mặt khác, lại có : \(EH\ge NP;FG\ge MQ\)
\(\Rightarrow EF+FG+GH+HE\ge\left(PM+MQ+BQ\right)+\left(PN+NP+BP\right)\)
\(=BD+BD=2\)
\(\Rightarrow EF+FG+GH+GE\ge2\) (dpcm)
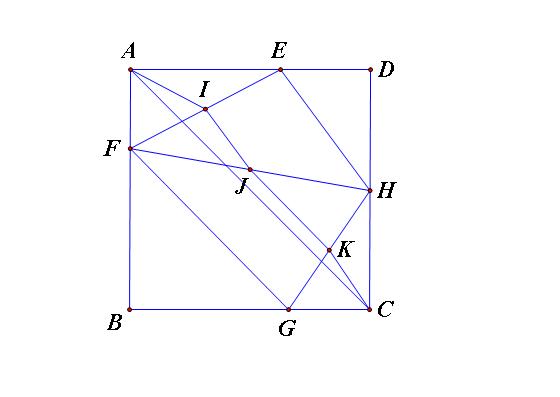
Ta có EF=2.AI,EH=2.IJ,GH=2.CK,EG=2.IK( Áp dụng tính chất đường trung bình và trung tuyến ứng với cạnh huyền trong tam giác vuông)
Suy ra \(P_{EFGH}=2\left(AI+IJ+JK+KC\right)\ge2AC=2\)
công thức tính đường chéo là \(\frac{n\left(n-3\right)}{2}\) với n là số cạnh
theo bài ra ta có \(\frac{n\left(n-3\right)}{2}=27\)
giải phương trình trên ta được n=9
vậy số cạnh của đa giác là 9 cạnh
bài này mình thi violympic rồi
Gọi n là số cạnh của đa giác, ta có công thức
n(n-3)/2=27
=>n=9