Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

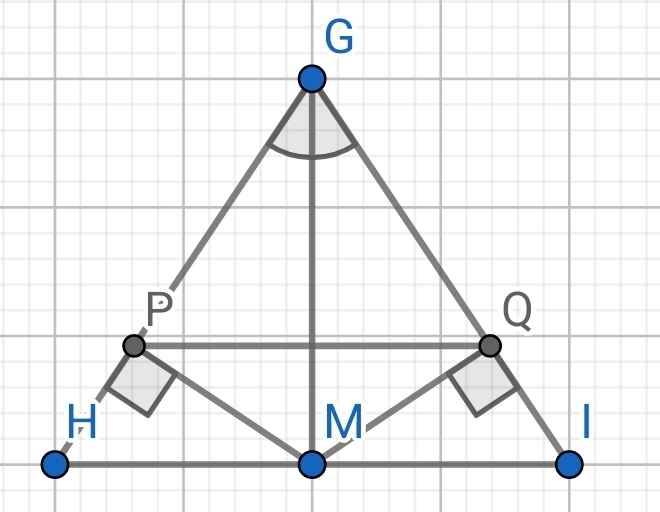 a) Do GM là tia phân giác của ∠HGI (gt)
a) Do GM là tia phân giác của ∠HGI (gt)
⇒ ∠HGM = ∠IGM
Xét ∆GHM và ∆GIM có:
GH = GI (do ∆GHI cân tại G)
∠HGM = ∠IGM (cmt)
GM là cạnh chung
⇒ ∆GHM = ∆GIM (c-g-c)
b) Do ∆GHM = ∆GIM (cmt)
⇒ HM = IM (hai cạnh tương ứng)
Do ∆GHM = ∆GIM (cmt)
⇒ ∠GMH = ∠GMI (hai góc tương ứng)
Mà ∠GMH + ∠GMI = 180⁰ (kề bù)
⇒ ∠GMH = ∠GMI = 180⁰ : 2 = 90⁰
⇒ GM ⊥ HI
c) Do ∠HGM = ∠IGM (cmt)
⇒ ∠PGM = ∠QGM
Xét hai tam giác vuông: ∆GMP và ∆GMQ có:
GM là cạnh chung
∠PGM = ∠QGM (cmt)
⇒ ∆GMP = ∆GMQ (cạnh huyền góc nhọn)
⇒ MP = MQ (hai cạnh tương ứng)
⇒ ∆MPQ cân tại M

x y A C D O B E
Kéo dài CO sao cho CO cắt DB tại E
Ta chứng minh được \(\Delta AOC=\Delta BOE\left(g-c-g\right)\)
\(\Rightarrow\) OC=OE và AC=BE
Mà \(B\in DE\) => BE+BD=DE => AC+BD=DE (1)
Do OC=OE mà \(O\in CE\) => O là trung điểm của CE. Mà \(OD\perp OC\Rightarrow OD\perp CE\) => OD là trung trực của CE => CD=ED (2)
Từ (1) và (2) => AC+BD=CD
Vậy CD=AC+BD

a) góc so le trong là XOA =OAB
b)XOA=AOB ( OA là tia phân giác góc O)
mặt khác AOB=OAB từ đó => BOA=BAO

A B C E D F 1 2
a) Vì BC2 = 102 = 100
AB2 + AC2 = 62 + 82 = 100
Nên AB2 + AC2 = BC2
Do đó: \(\Delta ABC\) vuông tại A
b) Xét hai tam giác vuông ABD và EBD có:
BD: cạnh huyền chung
\(\widehat{B_1}=\widehat{B_2}\left(gt\right)\)
Vậy: \(\Delta ABD=\Delta EBD\left(ch-gn\right)\)
Suy ra: DA = DE (hai cạnh tương ứng)
c) \(\Delta DAF\) vuông tại A
=> DF > DA (đường vuông góc ngắn hơn đường xiên)
Mà DA = DE
Do đó: DF > DE (đpcm)
d) Xét hai tam giác vuông ABC và EBF có:
AB = EB (\(\Delta ABD=\Delta EBD\))
\(\widehat{B}\): góc chung
Vậy: \(\Delta ABC=\Delta EBF\left(cgv-gn\right)\)
\(\Rightarrow\) BF = BC (hai cạnh tương ứng)
\(\Rightarrow\) \(\Delta BFC\) cân tại B
\(\Rightarrow\) BD là đường phân giác đồng thời là đường trung trực của FC
Do đó: BD là đường trung trực của đoạn thẳng FC (đpcm).
a) Ta có :
\(6^2+8^2=10^2\\ \Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A ( Định lí Pi-ta-go đảo )
b) Xét \(\Delta DBA\) và \(\Delta DBE\),có :
Chung cạnh BD
\(\widehat{DBA}=\widehat{DBE}\)( BD là tia phân giác )
\(\Rightarrow\Delta BDA=\Delta BDE\left(ch-gn\right)\\ \Rightarrow DA=DE\)

hình tự vẽ nha bn mk lười quá vẽ cx dễ lắm
giải
a/ ta có: A+B+C=180\(^o\)
=> C = 180\(^o\)-B-A
C = 180\(^o\)-30-90
C = 60\(^o\)
Vậy C=60\(^o\)
c/ Do tia CD là tia P?G của góc C nên =>
Góc ADC = góc MCD( vì là 2 góc so le trong.
e/ ta có góc K vuông tại C nên
suy ra
K = 90\(^o\)
a: Xét ΔGHM và ΔGIM có
GH=GI
\(\widehat{HGM}=\widehat{IGM}\)
GM chung
Do đó: ΔGHM=ΔGIM
b: Ta có: ΔGHM=ΔGIM
nên MH=MI
Ta có: ΔGHI cân tai G
mà GM là đường trung tuyến
nên GM là đường cao
c: Xét ΔGPM vuông tại P và ΔGQM vuông tại Q có
GM chung
\(\widehat{PGM}=\widehat{QGM}\)
Do đó: ΔGPM=ΔGQM
Suy ra: MP=MQ
hay ΔMPQ cân tại M