NT
giúp mik với . TRL 1 câu cũng đc nha '-'
13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
NT
30 tháng 9 2021
ko sao à.mik kiểm tra lại thì thấy bạn đúng à.cảm ơn bạn nhiều 
25 tháng 8 2021
1) Ta có: Oz nằm giữa tia Ox và Oy
\(\Rightarrow\widehat{xOz}=\widehat{xOy}-\widehat{yOz}=120^0-30^0=90^0\)
=> Oz⊥Ox
2) Ta có: Ox' là tia đối của tia Ox
\(\Rightarrow\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-120^0=60^0\)(2 góc kề bù)
Ta có: Ox' là tia đối của tia Ox, Oy' là tia đối của tia Oy
\(\widehat{\Rightarrow x'Oy'}=\widehat{xOy}=120^0\)(2 góc đối đỉnh)
25 tháng 8 2021
1: Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOx}\)
nên tia Oz nằm giữa hai tia Ox và Oy
Suy ra: \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{xOz}=90^0\)
hay Ox\(\perp\)Oz
NT
1
MH
8 tháng 10 2021
c) \(2x=3y=5z\)⇒\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng tính chát dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y-z}{15+10-6}=\dfrac{95}{19}=5\)
⇒\(\left\{{}\begin{matrix}x=5.15=75\\y=5.10=50\\z=5.6=30\end{matrix}\right.\)
8 tháng 10 2021
a) Áp dụng t/c dtsbn:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{40}{20}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.7=14\\y=2.13=26\end{matrix}\right.\)
b) \(\dfrac{3}{x}=\dfrac{7}{y}\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
Và \(x+16=y\Rightarrow y-x=16\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{y-x}{7-3}=\dfrac{16}{4}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=4.3=12\\y=4.7=28\end{matrix}\right.\)
VA
2
24 tháng 12 2021
a: \(=\dfrac{1}{4}\cdot4-\dfrac{3}{4}\cdot\dfrac{4}{5}=1-\dfrac{3}{5}=\dfrac{2}{5}\)
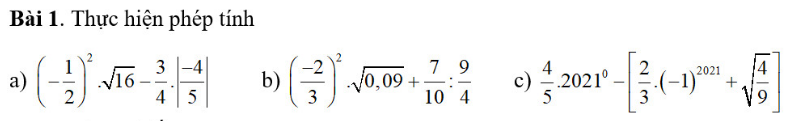
mà quá
8,
1,
\(\Delta MNP\)cân tại M
= > MN = MP , \(\widehat{N}=\widehat{P}\)
a, Xét \(\Delta MIN\perp I\)và \(\Delta MIP\perp I\)có :
\(MN=MP\left(gt\right)\)
\(\widehat{N}=\widehat{P}\left(gt\right)\)
= > \(\Delta MIN=\Delta MIP\left(ch-gn\right)\)
b, \(\Delta MIN=\Delta MIP\)( câu a, )
= > IN = IP ( 2 cạnh tương ứng )
2, \(\Delta MIN=\Delta MIP\)( câu a, phần 1 )
= > \(\widehat{NMI}=\widehat{PMI}\)( 2 góc tương ứng )
Xét \(\Delta LMI\)và \(\Delta KMI\)có :
\(MI\)chung
\(\widehat{NMI}=\widehat{PMI}\)( cmt )
= > \(\Delta LMI=\Delta KMI\left(ch-gn\right)\)
= > LI = KI ( 2 cạnh tương ứng )
Xét \(\Delta LIK\)có :
LI = KI
= > \(\Delta LIK\)cân tại I