K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GH
Gia Hân
VIP
7 tháng 7 2023
a) \(\dfrac{-7}{5}\) . \(\dfrac{4}{23}\) + \(\dfrac{4}{23}\) . \(\dfrac{2}{5}\)
= \(\dfrac{4}{23}\) . ( \(\dfrac{-7}{5}\) + \(\dfrac{2}{5}\) )
= \(\dfrac{4}{23}\) . -1
= \(\dfrac{-4}{23}\)
GH
Gia Hân
VIP
7 tháng 7 2023
b) \(\dfrac{-6}{7}\) . \(\dfrac{3}{5}\) +\(\dfrac{-6}{7}\) .\(\dfrac{2}{5}\) - \(1\dfrac{1}{3}\)
= \(\dfrac{-6}{7}\) . \(\dfrac{3}{5}\) +\(\dfrac{-6}{7}\) .\(\dfrac{2}{5}\) - \(\dfrac{4}{3}\)
= \(\dfrac{-6}{7}\) . (\(\dfrac{3}{5}\) + \(\dfrac{2}{5}\) ) - \(\dfrac{4}{3}\)
= \(\dfrac{-6}{7}\) . 1 - \(\dfrac{4}{3}\)
= \(\dfrac{-6}{7}\) - \(\dfrac{4}{3}\)
= \(\dfrac{-18}{21}\) - \(\dfrac{28}{21}\)
= \(\dfrac{-18}{21}\) + \(\dfrac{-28}{21}\)
= \(\dfrac{-46}{21}\)
DC
2
0
8 tháng 3 2019
a/b phải tối giản và phân số giữa tử và mẫu cách nhau 2 đơn vị
Bạn thử làm vậy xem
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2023
\(\dfrac{2n+15}{n+1}\in Z\Rightarrow2n+15⋮n+1\)
\(\Rightarrow2n+15-2\left(n+1\right)⋮n+1\)
\(\Rightarrow13⋮n+1\)
\(\Rightarrow n+1=Ư\left(13\right)\)
\(\Rightarrow n+1=\left\{-13;-1;1;13\right\}\)
\(\Rightarrow n=\left\{-14;-2;0;12\right\}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 3 2023
Cách hai: Theo bezout ta có: \(\dfrac{2n+15}{n+1}\) \(\in\) Z ⇔ 2.(-1) + 15 ⋮ n +1
⇔ 13 ⋮ n +1 ⇒ n + 1 \(\in\) { -13; -1; 1; 13} ⇒ n \(\in\) { -14; -2; 0; 12}
TH
8
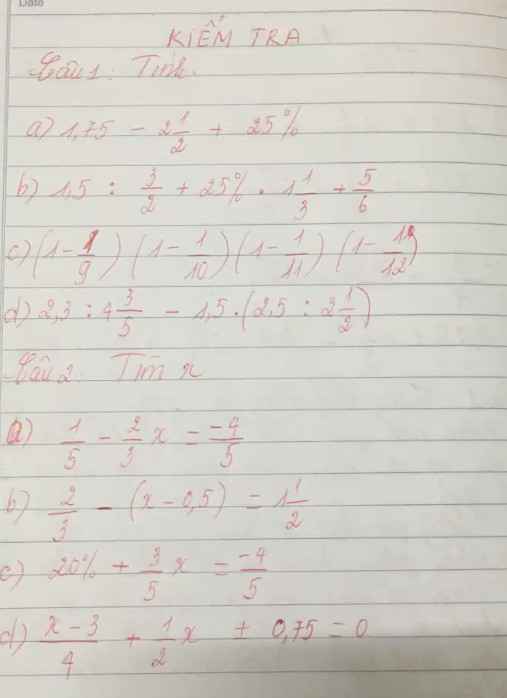
Lời giải:
$x^2+x+1=x(x-2)+3(x-2)+7=(x+3)(x-2)+7$
Để $(x+3)(x-2)+7\vdots x-2$ thì $7\vdots x-2$
Hay $x-2$ là ước của $7$
$\Rightarrow x-2\in\left\{1;-1;7;-7\right\}$
$\Rightarrow x\in\left\{3;1;9;-5\right\}$