
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(2sin^2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow-\left(1-2sin^2x\right)+\sqrt{3}sin2x=2\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
d, \(cosx-\sqrt{3}sinx=2cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow-2sin\dfrac{\pi}{3}.sinx=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)

23:
u4=10 và u7=22
=>\(\left\{{}\begin{matrix}u1+3d=10\\u1+6d=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3d=-12\\u1+3d=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}d=4\\u1=10-12=-2\end{matrix}\right.\)
=>Chọn C
Câu 22:
\(\left\{{}\begin{matrix}u1+2u5=0\\S_4=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1+2\left(u1+4d\right)=0\\4\cdot\dfrac{\left[2u1+3d\right]}{2}=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3u1+8d=0\\2u1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6u1+16d=0\\6u1+9d=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7d=-21\\2u_1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=-3\\2u_1=7-3d=7+9=16\end{matrix}\right.\)
=>\(u_1=8;d=-3\)
=>Chọn A
21A
19B

5.
\(sin\left(60^o+2x\right)=-1\)
\(\Leftrightarrow60^o+2x=-90^o+k.360^o\)
\(\Leftrightarrow x=-75^o+k.180^o\)
6.
\(sin\left(2x+1\right)=\dfrac{1}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=arcsin\dfrac{1}{3}+k2\pi\\2x+1=\pi-arcsin\dfrac{1}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}arcsin\dfrac{1}{3}-\dfrac{1}{2}+k\pi\\x=\dfrac{\pi}{2}-\dfrac{1}{2}arcsin\dfrac{1}{3}-\dfrac{1}{2}+k\pi\end{matrix}\right.\)
Cách làm :
sina = \(\dfrac{1}{2}\) ⇔ \(\left[{}\begin{matrix}a=\dfrac{\pi}{6}+k2\pi\\a=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
sina = \(-\dfrac{\sqrt{3}}{2}\) ⇔ \(\left[{}\begin{matrix}a=-\dfrac{\pi}{3}+k2\pi\\a=\dfrac{4\pi}{3}+k2\pi\end{matrix}\right.\)
sina = 1 ⇔ \(a=\dfrac{\pi}{2}+k.2\pi\)
sina = 0 ⇔ \(a=k\pi\)
sina = -1 ⇔ \(a=-\dfrac{\pi}{2}+k.2\pi\)
sina = \(\dfrac{1}{3}\) ⇔ \(\left[{}\begin{matrix}a=arcsin\left(\dfrac{1}{3}\right)+k2\pi\\a=\pi-arcsin\left(\dfrac{1}{3}\right)+k2\pi\end{matrix}\right.\)
Với a là một đa thức xác định trên R

\(\left|cosx\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\x=\pm\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)
\(\left|cosx\right|=\dfrac{1}{2}\)
\(\Leftrightarrow cos^2x=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1+cos2x}{2}=\dfrac{1}{4}\)
\(\Leftrightarrow cos2x=-\dfrac{1}{2}\)
\(\Rightarrow2x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Rightarrow x=\pm\dfrac{\pi}{3}+k\pi\)

1, \(\overrightarrow{v}=\overrightarrow{AB}=\left(1;3\right)\)
2, \(\overrightarrow{MM'}=\overrightarrow{v}=\left(2;3\right)\)
⇒ M' (3;6)
3, \(T_{\overrightarrow{v}}\left(d\right)=d'\) Ta có A(1 ; 0) ∈ d
⇒ \(\)d // d' và d đi qua A' = \(T_{\overrightarrow{v}}\left(A\right)\)
Tìm tọa độ A' rồi viết phương trình d' nhé




1.
\(sin^2x-4sinx.cosx+3cos^2x=0\)
\(\Rightarrow\dfrac{sin^2x}{cos^2x}-\dfrac{4sinx}{cosx}+\dfrac{3cos^2x}{cos^2x}=0\)
\(\Rightarrow tan^2x-4tanx+3=0\)
2.
\(\Leftrightarrow\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
3.
\(\Leftrightarrow2^2+m^2\ge1\)
\(\Leftrightarrow m^2\ge-3\) (luôn đúng)
Pt có nghiệm với mọi m (đề bài sai)
4.
\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow x-\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)
6.
ĐKXĐ: \(cosx\ne0\)
Nhân 2 vế với \(cos^2x\)
\(sin^2x-4cosx+5cos^2x=0\)
\(\Leftrightarrow1-cos^2x-4cosx+5cos^2x=0\)
\(\Leftrightarrow\left(2cosx-1\right)^2=0\)
\(\Leftrightarrow cosx=\dfrac{1}{2}\Rightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)

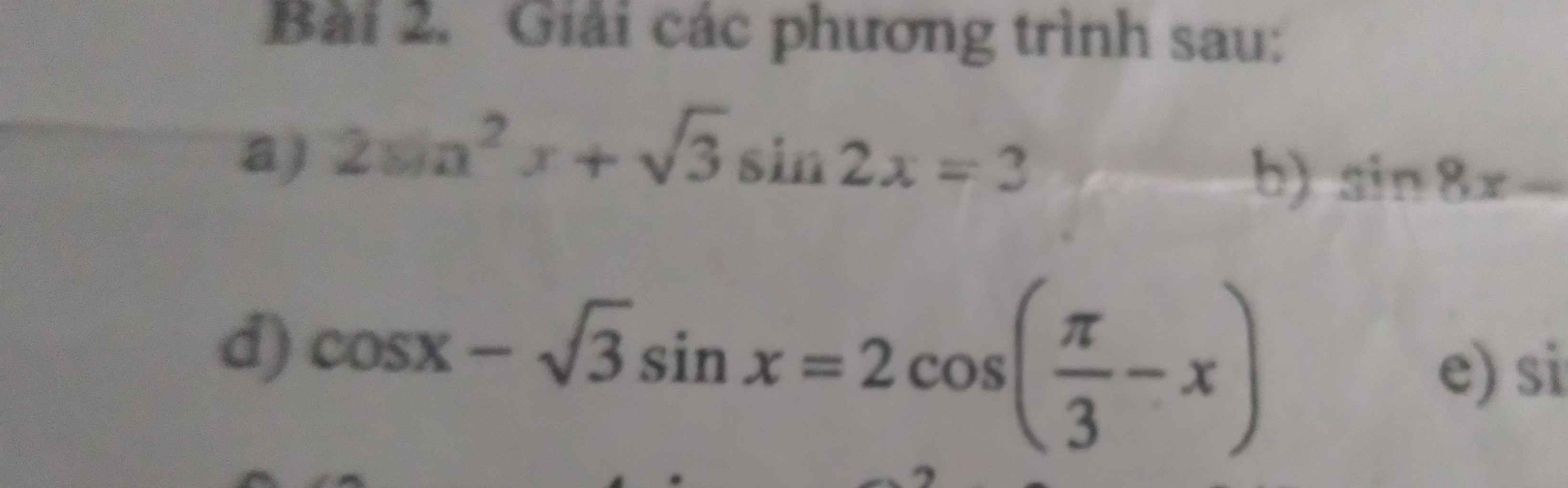












a.
Theo tính chất lập phương, \(CC'\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của \(AC'\) lên (ABCD)
\(\Rightarrow\widehat{C'AC}\) là góc giữa AC' và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=4\sqrt{2}\)
\(\Rightarrow tan\widehat{C'AC}=\dfrac{CC'}{AC}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{C'AC}\approx35^016'\)
b.
Theo t/c lập phương, \(CD\perp\left(BCB'\right)\)
Mà CD là giao tuyến (A'B'CD) và (ABCD)
\(\Rightarrow\widehat{BCB'}\) là góc giữa (A'B'CD) và (ABCD)
\(tan\widehat{BCB'}=\dfrac{BB'}{BC}=\dfrac{4}{4}=1\Rightarrow\widehat{BCB'}=45^0\)
c.
\(AA'\perp\left(A'B'C'D'\right)\Rightarrow AA'\perp A'P\Rightarrow\Delta MA'P\) vuông tại A'
\(\Rightarrow MP=\sqrt{A'M^2+A'P^2}=\sqrt{A'M^2+A'D'^2+D'P^2}\)
\(=\sqrt{2^2+4^2+2^2}=2\sqrt{6}\left(cm\right)\)
Tương tự:
\(MN=\sqrt{AM^2+AB^2+BN^2}=2\sqrt{6}\left(cm\right)\)
\(NP=\sqrt{C'P^2+C'C^2+CN^2}=2\sqrt{6}\left(cm\right)\)
\(\Rightarrow MN=MP=NP\Rightarrow\Delta MNP\) đều
\(\Rightarrow S_{\Delta MNP}=\dfrac{MN^2\sqrt{3}}{4}=6\sqrt{3}\left(cm^2\right)\)
d.
Gọi Q là trung điểm CD \(\Rightarrow PQ\perp\left(ABCD\right)\)
\(\Rightarrow\Delta ANQ\) là hình chiếu vuông góc của tam giác MNP lên (ABCD)
\(S_{\Delta ANQ}=S_{ABCD}-S_{ADQ}-S_{ABN}-S_{CNQ}\)
\(=AB^2-\dfrac{1}{2}AD.DQ-\dfrac{1}{2}AB.BN-\dfrac{1}{2}CQ.CN\)
\(=4^2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.2.2=6\left(cm^2\right)\)
\(\Rightarrow cos\alpha=\dfrac{S_{AQN}}{S_{MNP}}=\dfrac{6}{6\sqrt{3}}=\dfrac{1}{\sqrt{3}}\Rightarrow\alpha\approx54^044'\)