Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì a=1>0 nên để bpt có tập nghiệm R thì \(\Delta'\le0\)
\(\Leftrightarrow m^2-\left(6m-5\right)\le0\Leftrightarrow m^2-6m+5\le0\)
Lập bảng xét dấu suy ra \(1\le m\le5\)
Vậy có 5 giá trị nguyên của m để ...

Chọn A
TH1. Nếu m+ 3< 0 hay m< - 3.Khi đó :
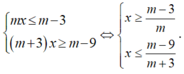
Hệ bất phương trình có nghiệm duy nhất

TH2. Nếu m+3= 0 hay m= -3
Khi đó :
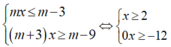
Hay x ≥ -2. Khi đó hệ bpt có vô số nghiệm (loại)
TH3. Nếu m+ 3> 0 hay m> - 3
+ Nếu -3< m< 0
Khi đó :
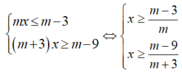
Hệ này có vô số nghiệm ( loại )
+ Nếu m= 0
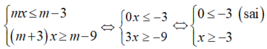
Hệ bất phương trình vô nghiệm( loại)
+ Nếu m> 0
Khi đó :
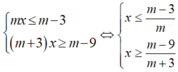
Hệ bất phương trình có nghiệm duy nhất
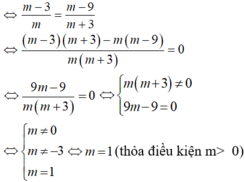
Vậy m= 1 thỏa yêu cầu bài toán.

* Nếu m= 0 thì bất phương trình đã cho trở thành:
0x < 0( luôn đúng với mọi x).
* Nếu m= 1 thì bất phương trình đã cho trở thành:
0x < 1 ( luôn đúng với mọi x)
Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}

a, Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-4m+4+m-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-\dfrac{3}{2}\right)^2< -\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
b, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-1\right)x^2+2\left(m-2\right)x-1< 0\) có nghiệm với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m-1< 0\\\Delta'=m^2-3m+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn

a/ \(\Delta'=\left(m-1\right)^2-3\left(m+4\right)< 0\)
\(\Leftrightarrow m^2-5m-11< 0\Rightarrow\frac{5-\sqrt{69}}{2}< m< \frac{5+\sqrt{69}}{2}\)
b/ \(\left\{{}\begin{matrix}m< 0\\\Delta=\left(m-1\right)^2-4m\left(m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\left(m-1\right)\left(3m+1\right)\ge0\end{matrix}\right.\) \(\Rightarrow m\le-\frac{1}{3}\)
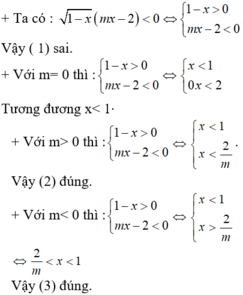
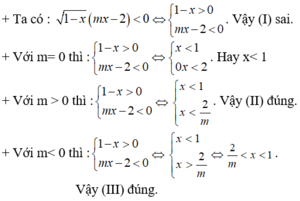

Đề bài thiếu bạn, BPT thiếu 1 vế, vế còn lại là \(\ge0;\le0,>0,< 0\)?