K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
VD
21 tháng 3 2022
a, Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{x}=\dfrac{5}{10}\Rightarrow x=4:\dfrac{1}{2}\Rightarrow x=8\)
Áp dụng hệ quả định lý Ta-lét ta có:
\(\dfrac{AE}{AC}=\dfrac{DE}{BC}\Rightarrow\dfrac{5}{15}=\dfrac{6}{y}\Rightarrow y=6:\dfrac{1}{3}\Rightarrow y=18\)
b, Áp dụng định lý phân giác ta có:
\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\Rightarrow\dfrac{5}{6}=\dfrac{10}{x}\Rightarrow x=10:\dfrac{5}{6}\Rightarrow x=12\)
30 tháng 7 2023
a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP)
=>ΔAMN đồng dạng với ΔNPC
VT
mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
1
28 tháng 6 2023
a: =x^2+6x+9+x^2-6x+9+2x^2-32
=4x^2-14
b: =(x+3-10+x)^2=(2x-7)^2=4x^2-28x+49
c: =(x-3-x+5)^2=2^2=4
e: =x^2+10x+25-x^2+10x-25=20x
d: A=(5-1)(5+1)(5^2+1)(5^4+1)/4
=(5^2-1)(5^2+1)(5^4+1)/4
=(5^4-1)(5^4+1)/4
=(5^8-1)/4
g: =x^2-9-x^2-4x+5
=-4x-4
4 tháng 1 2023
a: ĐKXĐ: x<>0; x<>1(A)
(B): x<>0; x<>3
(C): x<>2; x<>-2
b: \(A=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)
\(B=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)
\(C=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)
c: Khi x=0 thì A và B không xác định
Khi x=0 thì C=3/2
Khi x=3 thì B ko xác định, A=2/3; C=3/5
Y
4 tháng 1 2023
\(a,DKXD:\)
\(+x^2-x\ne0\Leftrightarrow x\ne0;1\)
\(+x^2-3x\ne0\Leftrightarrow x\ne0;3\)
+\(x^2-4\ne0\Leftrightarrow x\ne\pm4\)
\(b,\)
\(\dfrac{2x-2}{x^2-x}=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)
\(\dfrac{2x-6}{x^2-3x}=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)
\(\dfrac{3x-6}{x^2-4}=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)
\(c,\)
Vì phân thức 1,2 cùng kết quả nên mk lm 1 cái thôi nhé
+ Thay \(x=0\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{0}=0\)
Thay \(x=3\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{3}\)
+ Thay \(x=0\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{0+2}=\dfrac{3}{2}\)
Thay \(x=3\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{3+2}=\dfrac{3}{5}\)
6 tháng 3 2023
Bài 2:
Hình 3:
Xét ΔABC có AD là phân giác
nên x/3,5=7,2/4,5
=>x/3,5=1,8
=>x=6,3
Hình 4:
Xet ΔABC có MN//BC
nên 6/3=4/x
=>4/x=2
=>x=2
KV
6 tháng 3 2023
Bài 5
a) Ta có:
AB/A'B' = 6/4 = 3/2
AC/A'C' = 9/6 = 3/2
BC/B'C' = 12/8 = 3/2
⇒AB/A'B' = AC/A'C' = BC/B'C' = 3/2
⇒∆ABC ∽ ∆A'B'C' (c-c-c)
b) Do ∆ABC ∽ ∆A'B'C' (c-c-c)
⇒∠A = ∠A' = 100⁰
∠B = ∠B' = 44⁰
⇒∠C = 180⁰ - (∠A + ∠B)
= 180⁰ - (100⁰ + 44⁰)
= 36⁰
c) Tỉ số chu vi của ∆ABC và ∆A'B'C' là:
(AB + AC + BC)/(A'B' + A'C' + B'C')
= (6 + 9 + 12)/(4 + 6 + 8)
= 27/18
= 3/2
PL
3
30 tháng 8 2021
a)\(5x^2.\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right).\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y\\ =5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)\\ =27x^3+18x^2-12x-18x^2-12x+8=27x^3+8\)
30 tháng 8 2021
a) \(5x^2\left(10x^4-5x^3+2\right)=50x^6-25x^5+10x^2\)
b) \(\left(x^2-5x+3\right)\left(-5x\right)=-5x^3+25x^2-15x\)
c) \(\left(5x-2y\right)\left(x^2-xy+1\right)=5x^3-5x^2y+5x-2x^2y+2xy^2-2y=5x^3-7x^2y+2xy^2+5x-2y\)
d) \(\left(3x-2\right)\left(9x^2+6x-4\right)=27x^3+18x^2-12x-18x^2-12x+8=27x^3-24x+8\)
23 tháng 5 2022
a, ta có A(x)=2x3+7x2+ax+b
=(2x3+2x2+2x)+(5x2+5x+5)+ax-7x+b-5
=2x(x2+x+1)+5(x2+x+1)+(a-7)x+(b-5)
=(x2+x+1)(2x+5)+(a-7)x+(b-5)
ta có: (x2+x+1)(2x+5)⋮B(x)
→để A(x)⋮B(x) thì (a-7)x+(b-5)=0
→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)
vậy ....
mk trình bày hơi tắt xíu
bn cố gắng dịch nhé
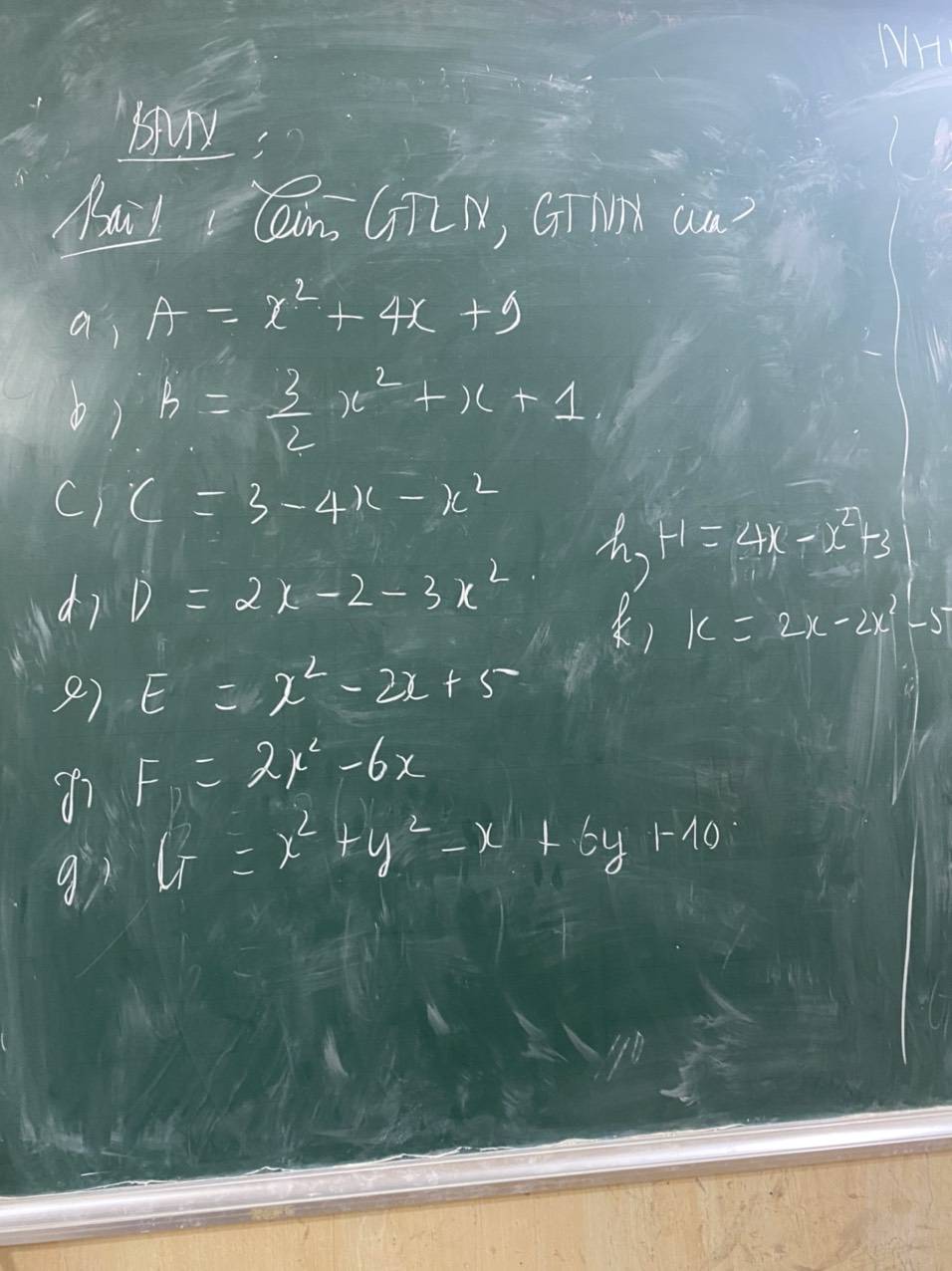
a: A=x^2+4x+4+5
=(x+2)^2+5>=5
Dấu = xảy ra khi x=-2
b: =3/2(x^2+2/3x+2/3)
=3/2(x^2+2*x*1/3+1/9+5/9)
=3/2(x+1/3)^2+15/18>=15/18=5/6
Dấu = xảy ra khi x=-1/3
e: =x^2-2x+1+4
=(x-1)^2+4>=4
Dấu = xảy ra khi x=1
f: =2(x^2-3x)
=2(x^2-3x+9/4-9/4)
=2(x-3/2)^2-9/2>=-9/2
Dấu = xảy ra khi x=3/2
h: =-(x^2-4x-3)
=-(x^2-4x+4-7)
=-(x-2)^2+7<=7
Dấu = xảy ra khi x=2