
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều


Bài 1:
Kẻ \(OM\perp AB\), \(OM\)cắt \(CD\)tại \(N\).
Khi đó \(MN=8cm\).
TH1: \(AB,CD\)nằm cùng phía đối với \(O\).
\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (1)
\(R^2=OA^2=OM^2+AM^2=\left(h+8\right)^2+\left(\frac{15}{2}\right)^2\)(2)
Từ (1) và (2) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{9}{4}\).
TH2: \(AB,CD\)nằm khác phía với \(O\).
\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (3)
\(R^2=OA^2=OM^2+AM^2=\left(8-h\right)^2+\left(\frac{15}{2}\right)^2\)(4)
Từ (3) và (4) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{-9}{4}\)(loại).
Bài 3:
Lấy \(A'\)đối xứng với \(A\)qua \(Ox\), khi đó \(A'\)có tọa độ là \(\left(1,-2\right)\).
\(MA+MB=MA'+MB\ge A'B\)
Dấu \(=\)xảy ra khi \(M\)là giao điểm của \(A'B\)với trục \(Ox\).
Suy ra \(M\left(\frac{5}{3},0\right)\).






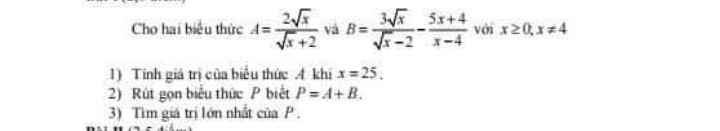





 Mọi người giúp em bài này với ạ.EM cần gấp ạ
Mọi người giúp em bài này với ạ.EM cần gấp ạ Mọi người giúp em bài này với ạ.EM cần gấp ạ
Mọi người giúp em bài này với ạ.EM cần gấp ạ



1: Khi x=25 thì A=(2*5)/(5+2)=10/7
2: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}}{\sqrt{x}-2}-\dfrac{5x+4}{x-4}\)
\(=\dfrac{2x-4\sqrt{x}+3x+6\sqrt{x}-5x-4}{x-4}=\dfrac{2\left(\sqrt{x}-2\right)}{x-4}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
3: căn x+2>=2
=>P<=2/2=1
Dấu = xảy ra khi x=0