
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
∠A₁ + ∠A₂ = 180⁰ (kề bù)
⇒ ∠A₂ = 180⁰ - ∠A₁ (1)
Lại có:
∠A₁ + ∠B₁ = 180⁰
⇒ ∠B₁ = 180⁰ - ∠A₁ (2)
Từ (1) và (2) ⇒ ∠A₂ = ∠B₁
Mà ∠A₂ và ∠B₁ là hai góc so le trong
⇒ a // b
4:
\(\widehat{A_1}=\widehat{A_3}\)(đối đỉnh)
\(\widehat{A_1}+\widehat{B_1}=180^0\)
=>\(\widehat{A_3}+\widehat{B_1}=180^0\)
mà hai góc này ở vị trí trong cùng phía
nên a//b

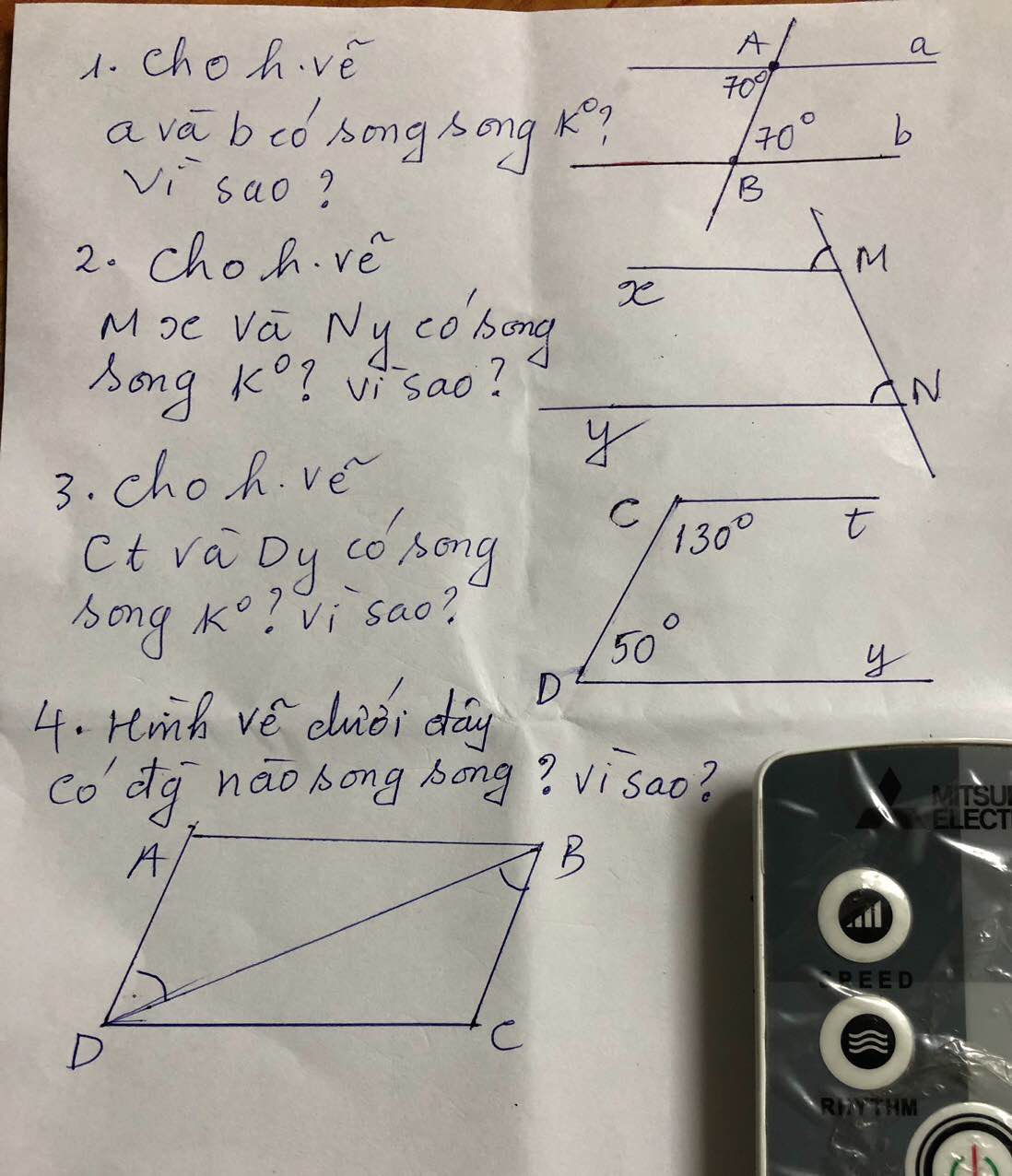
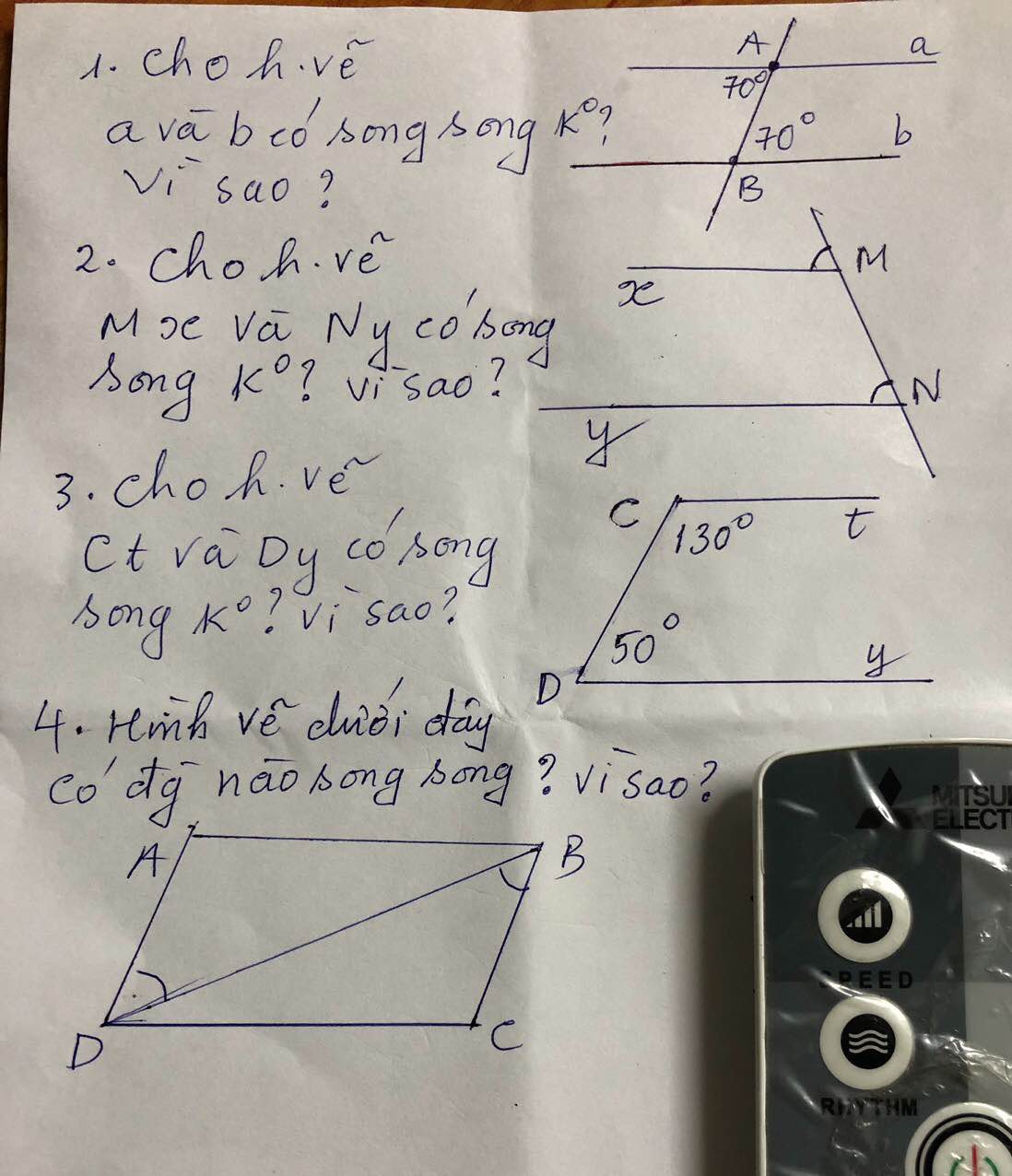
4) Ta có: ADB = BDC
Mà 2 góc này ở vị trí so le trong
=> AB//CD
Đúng thì like giúp mik nhé. Thx bạn
3) Dy//Ct vì \(\widehat{tCd}+\widehat{yDC}=180^0\) và \(\widehat{tCd}\); \(\widehat{yDC}\) là hai góc trong cùng phía

1, a và b có song song vì \(\)có 2 góc =70 độ ở vị trí so le trong
2.Mx và Ny có song song do góc M =góc N và 2 góc ở vị trí đônhg vị
3.Ct và Dy có song song vì góc C+ góc D=180 độ và 2 góc này ở vị trí trong cùng phía
4. có AD song song BC vì góc ADB=góc DBC
và 2 góc ở vị trí so le trong
4:
Có: Góc ADB = Góc DBC (GT)
Mà 2 góc này là 2 góc so le trong
=> AD // BC

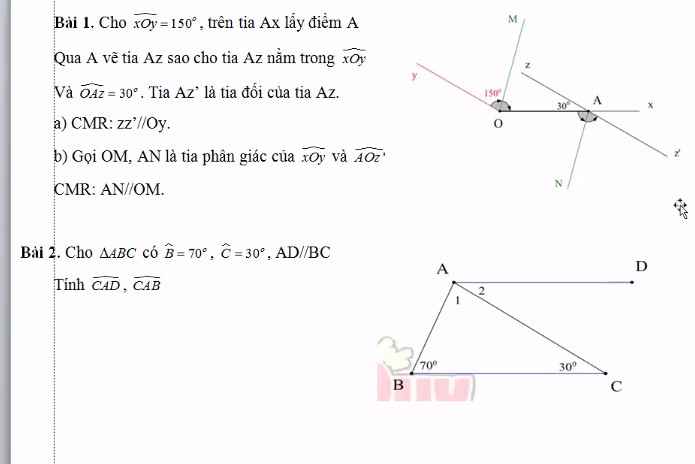
a) Ta có: \(\widehat{BAC}+\widehat{xAC}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xAC}=100^0\)
\(\Leftrightarrow\widehat{xAt}=\widehat{CAt}=\dfrac{\widehat{xAC}}{2}=\dfrac{100^0}{2}=50^0\)
b) Ta có: \(\widehat{CAt}=\widehat{BCA}\left(=50^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên At//BC(Dấu hiệu nhận biết hai đường thẳng song song)


OM\(\perp\)AB
=>\(\widehat{MOA}=\widehat{MOB}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOE}< \widehat{AOM}\)
nên tia OE nằm giữa hai tia OA và OM
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{AOM}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OB, ta có: \(\widehat{BOF}< \widehat{BOM}\)
nên tia OF nằm giữa hai tia OB và OM
=>\(\widehat{BOF}+\widehat{MOF}=\widehat{BOM}=90^0\)
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{BOF}+\widehat{MOF}\)
mà \(\widehat{AOE}=\widehat{BOF}\)
nên \(\widehat{MOE}=\widehat{MOF}\)
=>OM là phân giác của \(\widehat{EOF}\)

Có \(\frac{x}{y}=\frac{7}{10}\Rightarrow\frac{x}{7}=\frac{y}{10}\) . Áp dụng tính chất dãy tỉ số bằng nhau, ta có :
\(\frac{x}{7}=\frac{y}{10}=\frac{x+y}{7+10}=\frac{34}{17}=2\) . Từ đó ta suy ra được
\(\Rightarrow x=2.7=14\) \(\Rightarrow y=2.10=20\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BC=6cm
nên BM=3cm
=>AM=4cm
d: Xét ΔABC cân tại A có AM là đường cao
nên AM là phân giác của góc BAC
Xét ΔABC có
AM là đường phân giác
BI là đường phân giác
AM cắt BI tại I
Do đó: CI là tia phân giác của góc ACB
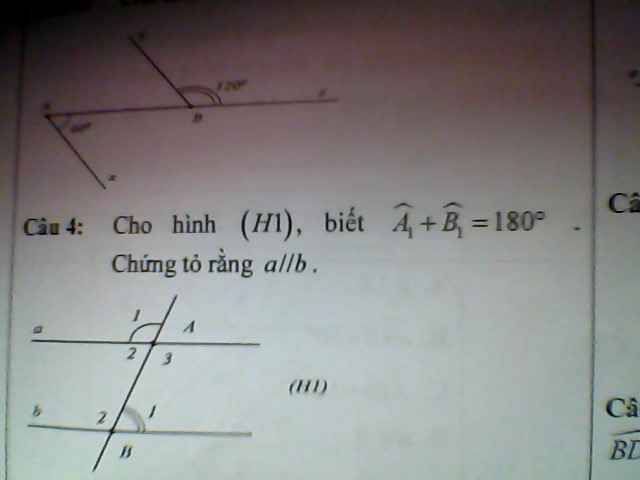


 mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
A) (-2/3)^4 = -2^4/3^4 = 16/81
3.27.9=3.3^3.3^2=3^6
Còn lại tự làm