K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 9 2021
4: Ta có: \(x^2+10x+25=0\)
\(\Leftrightarrow x+5=0\)
hay x=-5
5: Ta có: \(x^2-x+\dfrac{1}{4}=0\)
\(\Leftrightarrow x-\dfrac{1}{2}=0\)
hay \(x=\dfrac{1}{2}\)
6: Ta có: \(x^2-10x+25=0\)
nên x-5=0
hay x=5
TS
2
30 tháng 10 2023
\(\widehat{x'MC}=\widehat{xMN}\)(hai góc đối đỉnh
mà \(\widehat{xMN}=60^0\)
nên \(\widehat{x'MC}=60^0\)
Mz là phân giác của \(\widehat{x'MC}\)
=>\(\widehat{x'Mz}=\widehat{CMz}=\dfrac{60^0}{2}=30^0\)
Mz//Nt
=>\(\widehat{zMC}=\widehat{tNM}\)(hai góc đồng vị)
=>\(\widehat{tNM}=30^0\)
Nt là phân giác của góc y'NM
=>\(\widehat{y'NM}=2\cdot\widehat{tMN}=60^0\)
HD
0
12 tháng 11 2021
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a-b}{6-4}=\dfrac{30}{2}=15\)
Do đó: a=90; b=60; c=45
13 tháng 7 2021
\(\frac{3}{13}.\frac{5}{9}+\frac{1}{6}:\frac{13}{3}+1\)
\(=\frac{3}{13}.\frac{5}{9}+\frac{1}{6}.\frac{3}{13}+1\)
\(=\frac{3}{13}.\left(\frac{5}{9}+\frac{1}{6}\right)+1\)
\(=\frac{3}{13}.\left(\frac{30+9}{54}\right)+1\)
\(=\frac{3}{13}.\frac{39}{54}+1\)
\(=\frac{1}{6}+1\)
\(=\frac{7}{6}\)
\(\frac{5}{6}-\frac{7}{9}.\frac{2}{13}-\frac{7}{9}.\frac{11}{13}+\frac{-2}{9}\)
\(=\frac{5}{6}-\frac{7}{9}.\left(\frac{2}{13}-\frac{11}{13}\right)+\frac{-2}{9}\)
\(=\frac{5}{6}-\frac{7}{9}.\frac{-9}{13}-\frac{2}{9}\)
\(=\frac{5}{6}-\frac{-7}{13}-\frac{2}{9}\)
\(\frac{5}{6}-\frac{7}{9}.\frac{2}{13}-\frac{7}{9}.\frac{11}{13}+\frac{-2}{9}\)
\(=\frac{5}{6}-\frac{7}{9}.\left(\frac{2}{13}-\frac{11}{13}\right)+\frac{-2}{9}\)
\(=\frac{5}{6}-\frac{7}{9}.\frac{-9}{13}-\frac{2}{9}\)
\(=\frac{5}{6}-\frac{-7}{13}-\frac{2}{9}\)
\(=\frac{5}{6}+\frac{7}{13}-\frac{2}{9}\)
\(=\frac{195+126-52}{234}\)
\(=\frac{269}{234}\)
13 tháng 7 2021
\(\frac{3}{13}.\frac{5}{9}+\frac{1}{6}:\frac{13}{3}+1\)
\(=\frac{3}{13}.\frac{5}{9}+\frac{1}{6}.\frac{3}{13}+1\)
\(=\frac{3}{13}.\left(\frac{5}{9}+\frac{1}{6}\right)+1\)
\(=\frac{3}{13}.\left(\frac{30+9}{54}\right)+1\)
\(=\frac{3}{13}.\frac{39}{54}+1\)
\(=\frac{1}{6}+1=\frac{1}{6}+\frac{6}{6}\)
\(=\frac{7}{6}\)
\(\frac{-7}{9}.\frac{2}{13}-\frac{7}{9}.\frac{11}{13}+\frac{-2}{9}\)
\(=\frac{-7}{9}.\frac{2}{13}+\frac{-7}{9}.\frac{11}{13}+\frac{-2}{9}\)
\(=\frac{-7}{9}.\left(\frac{2}{13}+\frac{11}{13}\right)+\frac{-2}{9}\)
\(=\frac{-7}{9}.1+\frac{-2}{9}\)
\(=\frac{-7}{9}+\frac{-2}{9}\)
\(=\frac{-9}{9}=-1\)
\(\frac{2}{13}.\frac{2}{7}.5\)
\(=\frac{2.2.5}{13.7}\)
\(=\frac{20}{91}\)
\(\frac{1}{5}.\frac{11}{12}.\frac{21}{6}\)
\(=\frac{11.21}{5.12.6}\)
\(=\frac{231}{360}=\frac{77}{120}\)
17 tháng 8 2021
Bài 6:
a:
Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAC}\)
b: Xét ΔAKD vuông tại K và ΔAHD vuông tại H có
AD chung
\(\widehat{KAD}=\widehat{HAD}\)
Do đó: ΔAKD=ΔAHD
Suy ra: AK=AH
23 tháng 8 2018
1) = \(\frac{3}{5}\)
2) =\(\frac{6}{7}\)
3)\(\frac{9}{13}\)
4)\(\frac{4}{13}\)
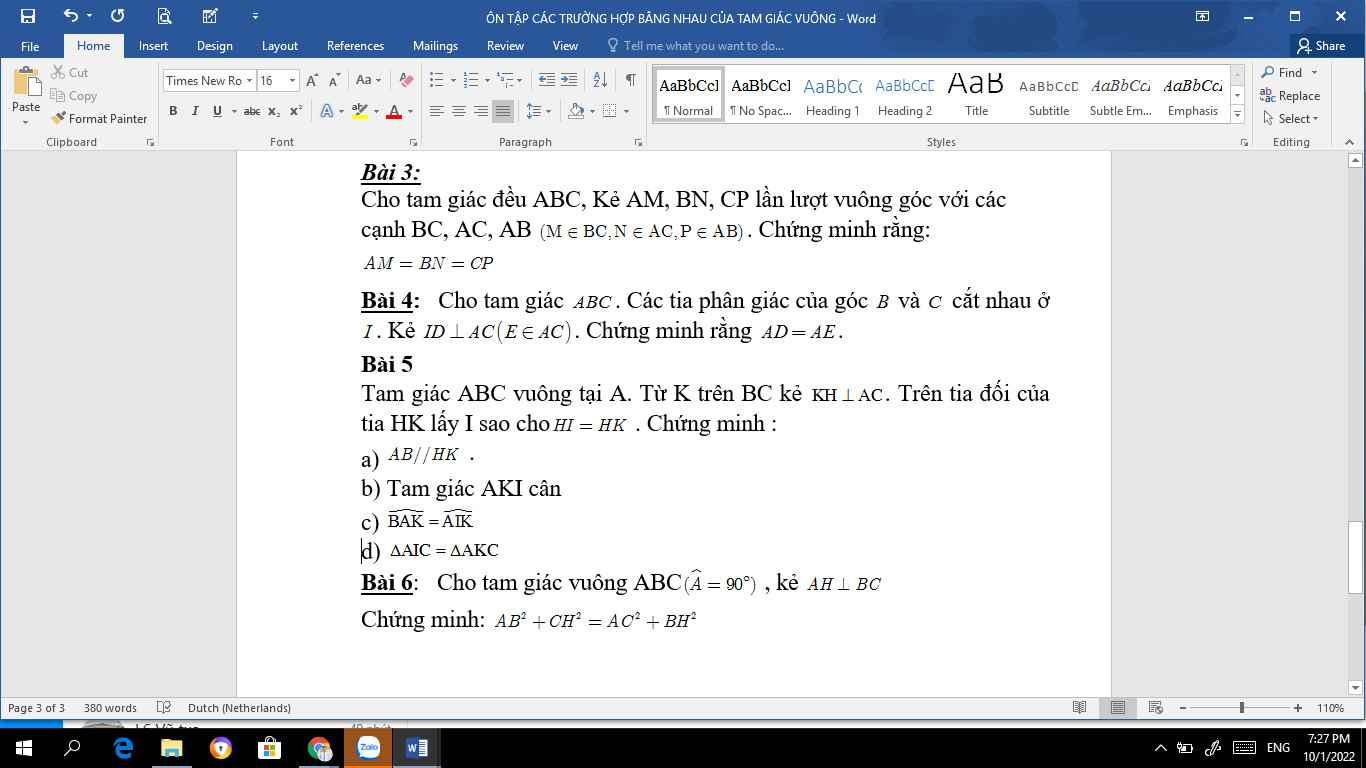
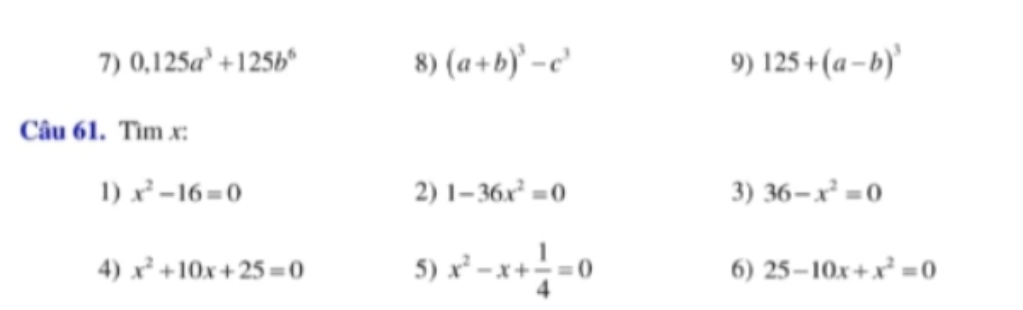
Bài 6:
Xét ΔABH vuông tại H có
\(AH^2+HB^2=AB^2\)
nên \(AB^2-HB^2=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có
\(AH^2+HC^2=AC^2\)
hay \(AC^2-HC^2=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AB^2-HB^2=AC^2-HC^2\)
hay \(AB^2+HC^2=AC^2+HB^2\)
bn ko làm câu 5 à?