
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét ΔABH vuông tại H có
\(AB^2=AH^2+HB^2\)
hay AH=12(cm)
Xét ΔAHB vuông tại H có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{5}{13}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{12}{5}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{5}{12}\)


Theo như hình vẽ thì I là tâm đường tròn ngoại tiếp ABC và J là giao điểm MI với AO đúng không nhỉ?
Tam giác AMJ vuông tại J nên theo Pitago: \(MJ^2=MA^2-AJ^2\)
Tương tự tam giác vuông MJO: \(MJ^2=MO^2-JO^2\)
Trừ vế theo vế: \(MA^2-AJ^2-MO^2+JO^2=0\) (1)
Tam giác vuông AIJ: \(IJ^2=AI^2-AJ^2\)
Tam giác vuông \(IJO\): \(IJ^2=OI^2-JO^2\)
\(\Rightarrow AI^2-AJ^2-OI^2+JO^2=0\) (2)
Trừ vế (1) và (2): \(MA^2-AI^2-MO^2+OI^2=0\) (3)
Do O là trung điểm BC nên \(IO\perp BC\)
\(\Rightarrow OI^2+OC^2=IC^2\)
Do M, C cùng thuộc đường tròn tâm O đường kính BC \(\Rightarrow OC=OM\)
Do I là tâm đường tròn ngoại tiếp ABC \(\Rightarrow IC=IA\)
\(\Rightarrow OI^2+OM^2=IA^2\Rightarrow OI^2-IA^2=-OM^2\)
Thế vào (3):
\(MA^2-MO^2-MO^2=0\Rightarrow MA=MO\sqrt{2}=\dfrac{BC\sqrt{2}}{2}\Rightarrow BC=\sqrt{2}MA\)
Em vẽ hình ra được không nhỉ? Hiện tại đang không có công cụ vẽ hình nên không hình dung được dạng câu c

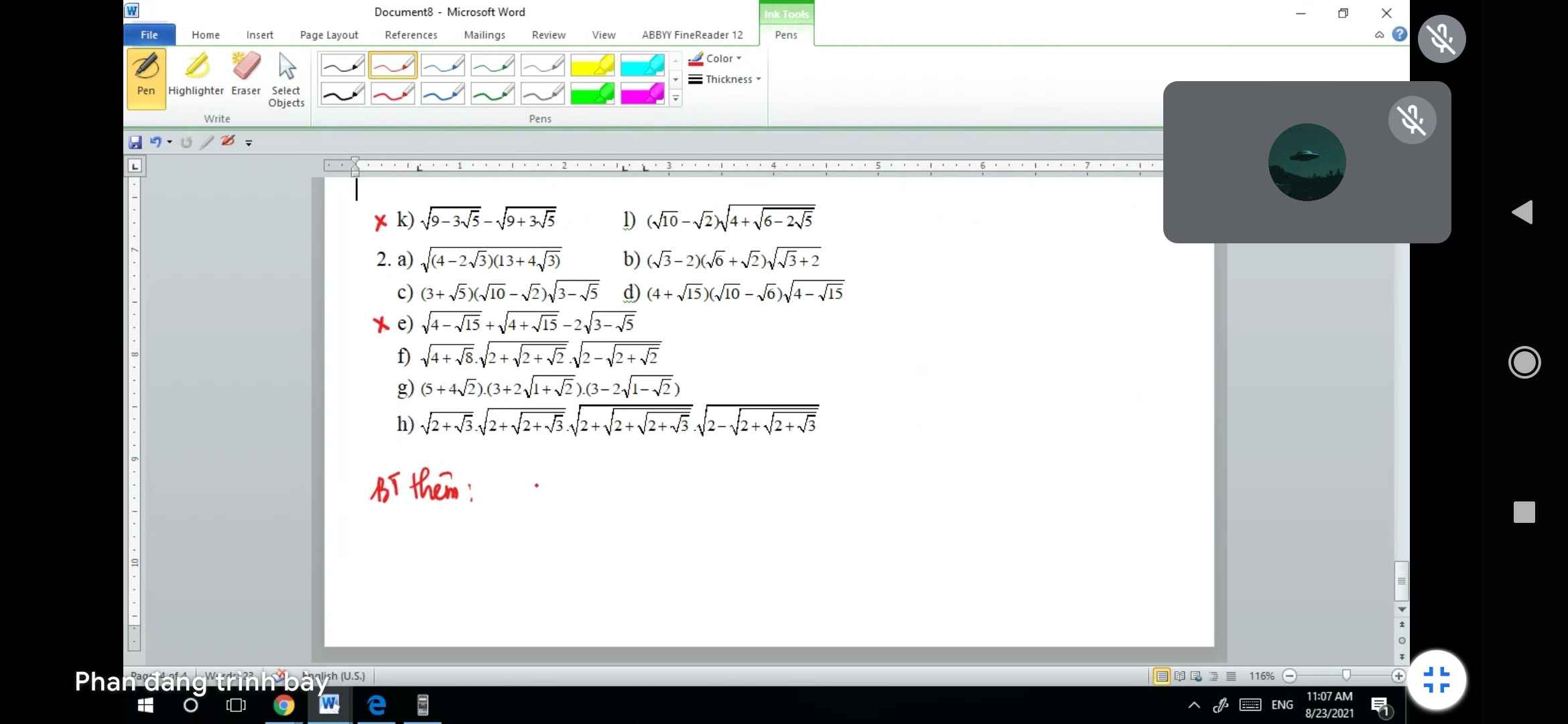
\(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}=\dfrac{1}{\sqrt{2}}\left(\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{15}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{15}+\sqrt{3}\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}\right)=-\dfrac{2\sqrt{3}}{\sqrt{2}}=-\sqrt{6}\)
\(\sqrt{4-\sqrt{15}}+\sqrt{4+\sqrt{15}}-2\sqrt{3-\sqrt{5}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{15}}+\sqrt{8+2\sqrt{15}}-2\sqrt{6-2\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}-2\sqrt{\left(\sqrt{5}-1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-\sqrt{3}+\sqrt{5}+\sqrt{3}-2\left(\sqrt{5}-1\right)\right)\)
\(=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
k: Ta có: \(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}\)
\(=\dfrac{\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}}{\sqrt{2}}\)
\(=-\sqrt{6}\)

a: \(Q=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{x-4}:\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{x-4}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\cdot\left(-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Khi x=4-2căn 3 thì \(Q=\dfrac{\sqrt{3}-1+2}{\sqrt{3}-1-3}=\dfrac{\sqrt{3}+1}{\sqrt{3}-4}=\dfrac{-7-5\sqrt{3}}{13}\)
c: Q>1/6
=>Q-1/6>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{1}{6}>0\)
=>\(\dfrac{6\sqrt{x}+12-\sqrt{x}+3}{6\left(\sqrt{x}-3\right)}>0\)
=>\(\dfrac{5\sqrt{x}+9}{6\left(\sqrt{x}-3\right)}>0\)
=>căn x-3>0
=>x>9
 Giúp mik câu 10 , 12 với nha
Giúp mik câu 10 , 12 với nha
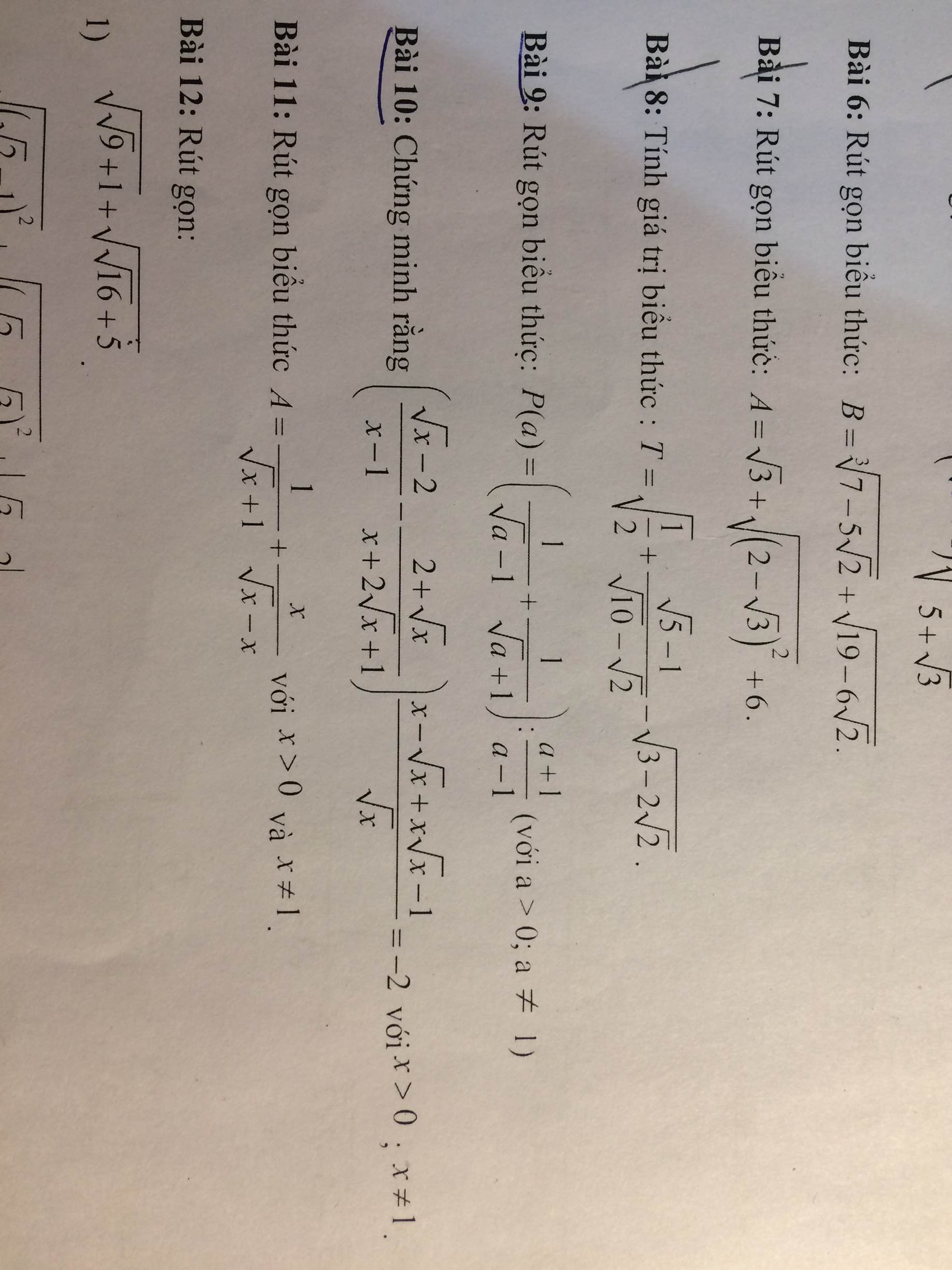



\(10,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x^2+8+x^2+3-2\sqrt{\left(x^2+8\right)\left(x^2+3\right)}=4x^2-4x+1\\ \Leftrightarrow-2\sqrt{x^4+11x^2+24}=2x^2-4x-10\\ \Leftrightarrow-\sqrt{x^4+11x^2+24}=x^2-2x-5\\ \Leftrightarrow x^4+11x^2+24=\left(x^2-2x-5\right)^2\\ \Leftrightarrow x^4+11x^2+24=x^4+4x^2+25-4x^3+20x-10x^2\\ \Leftrightarrow4x^3+17x^2-20x-1=0\\ \Leftrightarrow4x^3-4x^2+21x^2-21x+x-1=0\\ \Leftrightarrow\left(x-1\right)\left(4x^2+21x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\4x^2+21x+1=0\left(1\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-21+5\sqrt{17}}{8}\\x=\dfrac{-21-5\sqrt{17}}{8}\end{matrix}\right.\)