K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 12 2023
a: Trong mp(ABCD), gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
b: Xét hình thang ADCB có
M,N lần lượt là trung điểm của AB,CD
=>MN là đường trung bình của hình thang ADCB
=>MN//AD//CB
Ta có: MN//CB
CB\(\subset\)(SBC)
MN không nằm trong mp(SBC)
Do đó: MN//(SBC)
Xét ΔASB có
M,P lần lượt là trung điểm của AB,AS
=>MP là đường trung bình của ΔASB
=>MP//SB
Ta có: SB//MP
MP\(\subset\)(MNP)
SB không nằm trong mp(MNP)
Do đó: SB//(MNP)
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔABC có
M,O lần lượt là trung điểm của AB,AC
=>MO là đường trung bình của ΔABC
=>MO//BC
Ta có: MN//BC
MO//BC
MN,MO có điểm chung là M
Do đó: M,N,O thẳng hàng
Xét ΔASC có
O,P lần lượt là trung điểm của AC,AS
=>OP là đường trung bình của ΔASC
=>OP//SC
ta có: SC//OP
OP\(\subset\)(MNP)
SC không nằm trong mp(MNP)
Do đó: SC//(MNP)
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
BA
1
20 tháng 7 2023
Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
\(y'=sinx+x.cosx\)
\(y''=cosx+cosx-x.sinx=2cosx-x.sinx\)
\(\Rightarrow xy-2\left(y'-sinx\right)+xy''=xy-2\left(sinx+x.cosx-sinx\right)+x\left(2cosx-x.sinx\right)\)
\(=xy-2x.cosx+2x.cosx-x^2sinx\)
\(=xy-x^2.sinx=x\left(xsinx\right)-x^2sinx=x^2sinx-x^2sinx=0\)
2 tháng 7 2023
a: AC=căn AB^2+BC^2=a*căn 2
A'B=căn AB^2+A'A^2=a*căn 5
A'C=căn A'A^2+AC^2=a*căn 6
Vì BC^2+BA'^2=A'C^2
nên ΔBA'C vuông tại B
b; B'C' vuông góc A'B'
B'C' vuông góc A'A
=>B'C' vuông góc (A'AB'A')
=>(AB'C') vuông góc (ABB'A')
c: (A'M;(ABC))=góc A'MA
tan A'MA=AA'/AM=4/căn 5
=>góc AMA'=61 độ
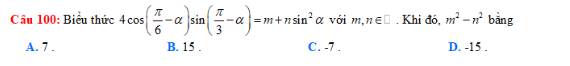
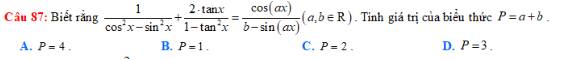
a: Xét (SAD) và (SBC) có
AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
b: Chọn mp(SCD) có chứa SC
Trong mp(ABCD), gọi E là giao điểm của AB và CD
\(M\in SD\subset\left(SCD\right);M\in\left(MAB\right)\)
=>\(M\in\left(SCD\right)\cap\left(AMB\right)\)
\(E\in CD\subset\left(SCD\right);E\in AB\subset\left(MAB\right)\)
Do đó: \(E\in\left(SCD\right)\cap\left(AMB\right)\)
Do đó: (SCD) giao (AMB)=ME
Gọi I là giao của SC với ME
=>I là giao điểm của SC với mp(MAB)