Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 7:
Giải:
Giá tiền của mỗi chiếc máy tính bán trong đợt đầu là:
8 x (100% + 30%) = 10,4(triệu đồng)
Tổng số tiền thu được khi bán 70 chiếc máy tính trong đợt đầu là:
10,4 x 70 = 728 (triệu đồng)
Giá của mỗi chiếc máy tính bán được trong đợt sau là:
10,4 x 65% = 6,76(triệu đồng)
Số tiền thu được khi bán hết số máy tính còn lại là:
6,76 x (100 - 70) = 202,8 (triệu đồng)
Tổng số tiền mà cửa hàng thu được khi bán hết 100 cái máy tính là:
728 + 202,8 = 930,8 (triệu đồng)
Tiền vốn của 100 cái máy tính là:
8 x 100 = 800 (triệu đồng)
Sau khi bán hết 100 máy tính thì người đó lãi và lãi số tiền là:
930,8 - 800 = 130,8 (triệu đồng)
Kết luận: Sau khi bán hết 100 máy tính người đó lãi và lãi số tiền là 130,8 triệu đồng
Bài 8:
a; Doanh thu năm 2019 là: 5,6 x \(\frac34\) = 4,2 (triệu usd)
b; Sau năm năm để lời 7,8 triệu usd thì năm 2020 phải thu được:
7,8 - (-1,8 + 5,6 - 3,6 + 4,2) = 3,4(triệu usd)
Kết luận: năm 2019 thu 4,2 triệu usd
năm 2020 thu 3,4 triệu usd

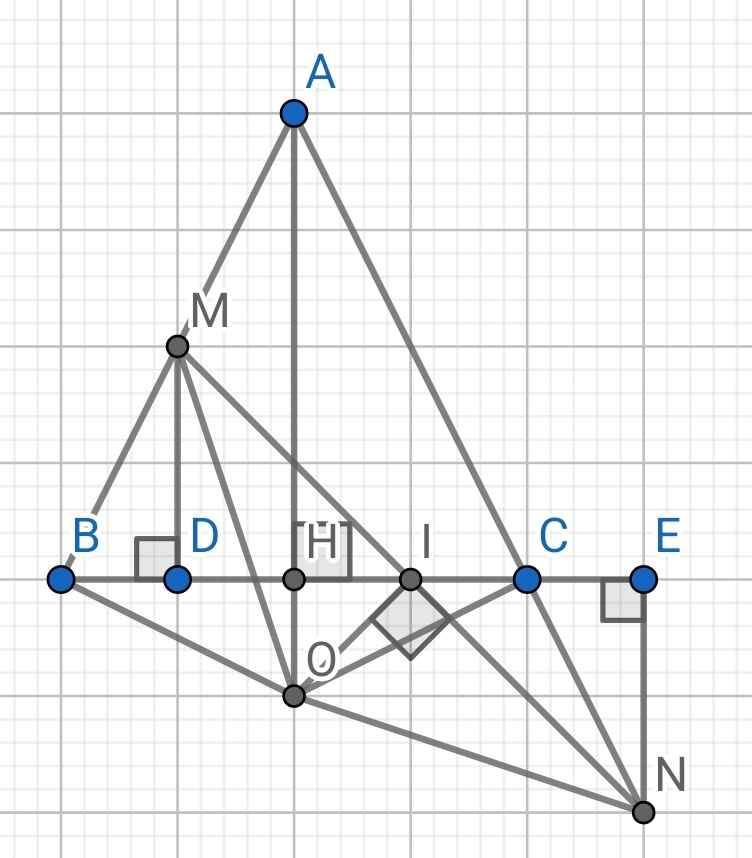 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC

 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC

Lời giải:
Trên $AC$ lấy $E$ sao cho $AB=AE$. Xét tam giác $ABD$ và $AED$ có:
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là tia phân giác $\widehat{A}$)
$AD$ chung
$AB=AE$
$\Rightarrow \triangle ABD=\triangle AED$ (c.g.c)
$\Rightarrow BD=DE(1)$ và $\widehat{ABD}=\widehat{AED}$
Có:
$\widehat{DEC}=180^0-\widehat{AED}=180^0-\widehat{ABD}=\widehat{ECD}+\widehat{BAC}> \widehat{ECD}$
$\Rightarrow DC> DE(2)$
Từ $(1); (2)\Rightarrow DC> DB$

\(\widehat{M_1}\) = \(\widehat{M_3}\) (hai góc đối đỉnh)
\(\widehat{M_3}\) + \(\widehat{N_1}\) = 1800 (hai góc trong cùng phía)
\(\widehat{M_3}\) = 1800 - \(\widehat{N_1}\)
\(\widehat{M_3}\) = 1800 - 500
\(\widehat{M_3}\) = 1300
⇒ \(\widehat{M_1}\) = 1300
Kết luận: \(\widehat{M_1}\) = 1300

a: \(5x\left(x-3\right)-x\left(5x+1\right)=16\)
=>\(5x^2-15x-5x^2-x=16\)
=>-16x=16
=>x=-1
b: \(4x\left(x-1\right)+x\left(3-4x\right)=5\)
=>\(4x^2-4x+3x-4x^2=5\)
=>-x=5
=>x=-5
c: \(5\left(x^2+4x-3\right)-x\left(5x+3\right)=19\)
=>\(5x^2+20x-15-5x^2-3x=19\)
=>17x=19+15=34
=>x=2







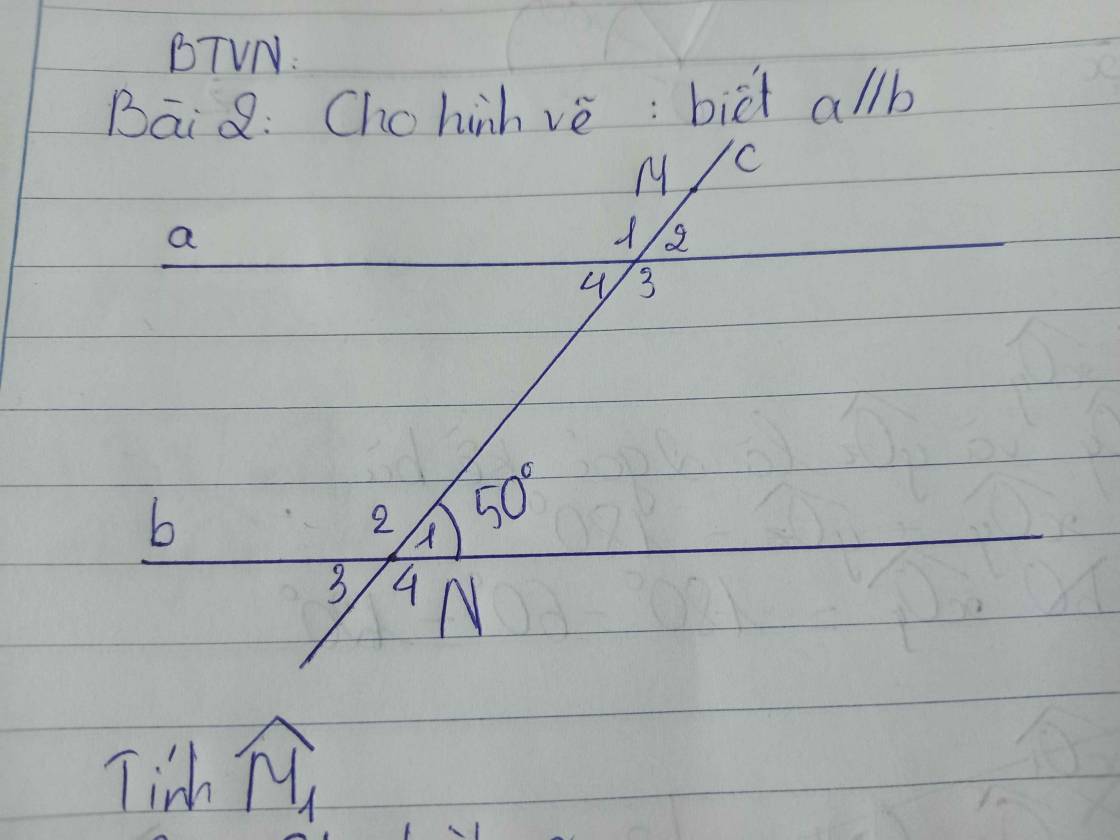

Bài 6
a) (3x² + 5) + [(2x² - 5x) - (5x² + 4)]
= 3x² + 5 + (2x² - 5x - 5x² - 4)
= 3x² + 5 + 2x² - 5x - 5x² - 4
= (3x² + 2x² - 5x²) - 5x + (5 - 4)
= -5x + 1
---------‐----------
b) (x + 2)(x² - 2x + 4)
= x.x² - x.2x + x.4 + 2.x² - 2.2x + 2.4
= x³ - 2x² + 4x + 2x² - 4x + 8
= x³ + (-2x² + 2x²) + (4x - 4x) + 8
= x³ + 8
-------------------
c) (4x³ - 8x² + 13x - 5) : (2x - 1)
= (4x³ - 2x² - 6x² + 3x + 10x - 5) : (2x - 1)
= [(4x³ - 2x²) - (6x² - 3x) + (10x - 5)] : (2x - 1)
= [2x²(2x - 1) - 3x(2x - 1) + 5(2x - 1)] : (2x - 1)
= (2x - 1)(2x² - 3x + 5) : (2x - 1)
= 2x² - 3x + 5