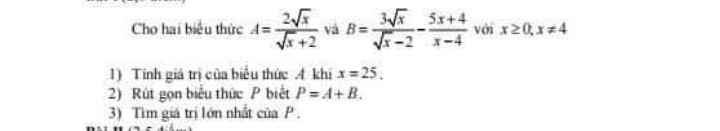K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HA
1
12 tháng 10 2021
\(\sqrt{x^2-2x+4}+\sqrt{x^2+5}=9-2x\left(đk:x\le\dfrac{9}{2}\right)\)
\(\Leftrightarrow x^2-2x+4+x^2+5+2\sqrt{\left(x^2-2x+4\right)\left(x^2+5\right)}=81-36x+4x^2\)
\(\Leftrightarrow2\sqrt{\left(x^2-2x+4\right)\left(x^2+5\right)}=2x^2-34x+72\)
\(\Leftrightarrow4\left(x^2-2x+4\right)\left(x^2+5\right)=4x^4+1156x^2+5184-136x^3+288x^2-4896x\)
\(\Leftrightarrow4x^4-8x^3+36x^2-40x+80=4x^4-136x^3+1444x^2-4896x+5184\)
\(\Leftrightarrow128x^3-1408x^2+4856x-5104=0\)
\(\Leftrightarrow128x^2\left(x-2\right)-1152x\left(x-2\right)+2552\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(128x^2-1152x+2552\right)=0\)
\(\Leftrightarrow x=2\left(tm\right)\)(do \(128x^2-1152x+2552>0\))
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(\left(xy+3\right)^2+\left(x+y\right)^2=8\)
\(\Leftrightarrow x^2y^2+x^2+y^2+1=-8xy\)
\(\dfrac{x}{x^2+1}+\dfrac{y}{y^2+1}=-\dfrac{1}{4}\Leftrightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{x^2y^2+x^2+y^2+1}=-\dfrac{1}{4}\)
\(\Rightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{-8xy}=-\dfrac{1}{4}\)
\(\Rightarrow\left(xy+1\right)\left(x+y\right)=2xy\)
\(\Rightarrow x+y=\dfrac{2xy}{xy+1}\)
Thế vào pt ban đầu:
\(\left(xy+3\right)^2+\left(\dfrac{2xy}{xy+1}\right)^2=8\)
Đặt \(xy+1=t\Rightarrow\left(t+2\right)^2+4\left(\dfrac{t-1}{t}\right)^2=8\)
\(\Rightarrow\left(t^2+2t\right)^2-4\left(t^2+2t\right)+4=0\)
\(\Leftrightarrow\left(t^2+2t-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1-\sqrt{3}\\t=-1+\sqrt{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}xy=-2-\sqrt{3}\Rightarrow x+y=1+\sqrt{3}\\xy=-2+\sqrt{3}\Rightarrow x+y=1-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow x;y\) là nghiệm của: \(\left[{}\begin{matrix}X^2-\left(1+\sqrt{3}\right)X-2-\sqrt{3}=0\\X^2-\left(1-\sqrt{3}\right)X-2+\sqrt{3}=0\end{matrix}\right.\)
\(\Rightarrow...\)
11 tháng 3 2022
a, bạn tự bạn
b, \(\Delta'=4\left(m+1\right)^2-\left(4m^2-2m-1\right)\)
\(=8m+4+2m+1=10m+5\)
Để pt có 2 nghiệm x1 ; x2 khi m >= -1/2
Ta có \(x_1+2x_2=4m^2+3-4m^2+2m+1=2m+4\)
Ta có hệ \(\left\{{}\begin{matrix}x_1+2x_2=2m+4\\x_1+x_2=4m+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2m\\x_1=4m+4-2m=2m+4\end{matrix}\right.\)
Thay vào ta được \(x_1x_2=4m^2-2m-1=2m\left(2m+4\right)\)
\(\Leftrightarrow-2m-1=8m\Leftrightarrow10m=-1\Leftrightarrow m=-\dfrac{1}{10}\)(tm)
11 tháng 3 2022
câu a ) thay m vào phương trình
câu b) tính giá trị của bài giữ nguyên phương trình
áp dụng định lí vi ét
rồi thay x1 x2 vào
29 tháng 8 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\). Gọi \(AB=2x\left(cm\right),AC=3x\left(cm\right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC:
\(BC^2=AB^2+AC^2=4x^2+9x^2=13x^2\)
\(\Rightarrow BC=\sqrt{13}x\)
Xét tam giác ABC vuông tại A có đường cao AH:
\(AH.BC=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow6\sqrt{13}x=6x^2\)
\(\Rightarrow x^2-\sqrt{13}x=0\)
Vì x > 0
\(\Rightarrow x=\sqrt{13}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AB=2x=2\sqrt{13}\left(cm\right)\\AC=3x=3\sqrt{13}\left(cm\right)\\BC=\sqrt{13}x=13\left(cm\right)\end{matrix}\right.\)
29 tháng 8 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\)
nên \(\dfrac{HB}{HC}=\dfrac{4}{9}\)
\(\Leftrightarrow HB=\dfrac{4}{9}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{4}{9}=36\)
\(\Leftrightarrow HC^2=16\)
\(\Leftrightarrow HC=4\left(cm\right)\)
\(\Leftrightarrow HB=9\left(cm\right)\)
Ta có: BH+HC=BC
nên BC=4+9=13(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}\left(cm\right)\\AC=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
VD
16 tháng 3 2022
\(a,\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2-4m+3\right)\\ =m^2+2m+1-m^2+4m-3\\ =6m-2\)
Để pt vô nghiệm thì \(6m-2< 0\Leftrightarrow m< \dfrac{1}{3}\)
Để pt có nghiệm kép thì \(6m-2=0\Leftrightarrow m=\dfrac{1}{3}\)
Để pt có 2 nghiệm phân biệt thì \(6m-2>0\Leftrightarrow m>\dfrac{1}{3}\)
\(b,\Delta=\left(m-3\right)^2-4.\left(-3m\right)\\ =m^2-6m+9+12m\\ =m^2+6m+9\\ =\left(m+3\right)^2\ge0\)
Suy ra pt luôn không vô nghiệm với mọi m
PT có nghiệm kép khi \(\left(m+3\right)^2=0\Leftrightarrow m=-3\)
PT có 2 nghiệm phân biệt khi \(\left(m+3\right)^2>0\Leftrightarrow m\ne-3\)
1 tháng 11 2021
\(a,=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\dfrac{\sqrt{21}}{7}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{4}\left(\sqrt{3}+\sqrt{2}\right)}=\dfrac{\sqrt{5}}{2}\\ c,=\dfrac{\sqrt{x}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{xy}}{y}\\ d,=\dfrac{\left(\sqrt{3}-\sqrt{2}\right)\left(2\sqrt{5}-\sqrt{3}\right)}{\left(2\sqrt{5}-\sqrt{3}\right)\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{3}-\sqrt{2}}{1-\sqrt{2}}\\ =\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+1\right)=2+\sqrt{2}-\sqrt{6}+\sqrt{3}\)
27 tháng 6 2023
1: Khi x=25 thì A=(2*5)/(5+2)=10/7
2: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}}{\sqrt{x}-2}-\dfrac{5x+4}{x-4}\)
\(=\dfrac{2x-4\sqrt{x}+3x+6\sqrt{x}-5x-4}{x-4}=\dfrac{2\left(\sqrt{x}-2\right)}{x-4}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
3: căn x+2>=2
=>P<=2/2=1
Dấu = xảy ra khi x=0
HH
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
Căn thức cuối cùng là \(\sqrt{1+x^2}\) hay \(\sqrt{1-x^2}\) vậy nhỉ?
\(\sqrt{1+x^2}\) thì bài này ko giải được