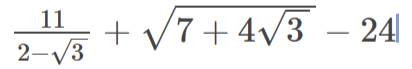K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
1
17 tháng 9 2021
a)
\(\sqrt{9+4\sqrt{5}}\cdot\sqrt{6-2\sqrt{5}}\\ =\sqrt{4+4\sqrt{5}+5}\cdot\sqrt{1-2\sqrt{5}+5}\\ =\sqrt{\left(2+\sqrt{5}\right)^2}\cdot\sqrt{\left(1-\sqrt{5}\right)^2}\\ =\left(2+\sqrt{5}\right)\left(1-\sqrt{5}\right)\)
b)
\(\sqrt{3+2\sqrt{2}}-\sqrt{6-4\sqrt{2}}\\ =\sqrt{2+2\sqrt{2}+1}-\sqrt{4-4\sqrt{2}+2}\\ =\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\left(2-\sqrt{2}\right)^2}\\ =\sqrt{2}+1-2+\sqrt{2}=2\sqrt{2}-1\)
6 tháng 5 2016
Lỗi nha bạn. Cái này bạn lên google tra. Có phải vô phần nghe là bị trục trặc hả?
6 tháng 5 2016
mình cũng cần người giúp mình khắc phục lỗi error 521 nữa]
NT
0
H
27 tháng 10 2023
\(\dfrac{11}{2-\sqrt{3}}+\sqrt{7+4\sqrt{3}}-24\\ =\dfrac{11\left(2+\sqrt{3}\right)}{4-3}+\sqrt{4+4\sqrt{3}+3}-24\\ =\dfrac{22+11\sqrt{3}}{1}+\sqrt{2^2+2\cdot2\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-24\\ =22+11\sqrt{3}+\sqrt{\left(2+\sqrt{3}\right)^2}-24\\ =22+11\sqrt{3}+2+\sqrt{3}-24\\ =12\sqrt{3}\)
DQ
5
DT
3
18 tháng 11 2018
KHÔNG ĐƯỢC ĐĂNG CÂU HỎI LINH TINH
NẾU ĐĂNG CÂU HỎI , CÁC THẦY CÔ TRÊN OLM SẼ TRỪ ĐIỂM .
18 tháng 11 2018
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
16 tháng 4 2021
Bài 17:
a) Xét tứ giác BDHF có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BDHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
16 tháng 4 2021
Bài 17:
b) Xét ΔABC có
AD là đường cao ứng với cạnh BC(gt)
CF là đường cao ứng với cạnh AB(gt)
AD cắt CF tại H(gt)
Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)
Suy ra: BH\(\perp\)AC
hay BE\(\perp\)AC
Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔFHB\(\sim\)ΔEHC(g-g)
Suy ra: \(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(HB\cdot HE=HC\cdot HF\)(đpcm)