
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Ta có: \(x-2\sqrt{x+8}=0\)
\(\Leftrightarrow\sqrt{4x+32}=x\)
\(\Leftrightarrow4x+32=x^2\)
\(\Leftrightarrow x^2-4x-32=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-4\left(loại\right)\end{matrix}\right.\)
b: Ta có: \(3\sqrt{x+5}=4x-7\)
\(\Leftrightarrow\left(4x-7\right)^2=9x+45\)
\(\Leftrightarrow16x^2-56x+49-9x-45=0\)
\(\Leftrightarrow16x^2-65x+4=0\)
\(\Leftrightarrow16x^2-64x-x+4=0\)
\(\Leftrightarrow\left(x-4\right)\left(16x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{16}\end{matrix}\right.\)

câu a : căn hai phần 2-5x có nghĩa ↔2 phần 2-5x lớn hơn hoặc bằng 0 ↔2-5x lớn hơn 0↔x nhỏ hơn 2 phần 5 câu b: căn 5-2x phần x2 có nghĩa ↔5-2x >= 0↔ x<= 5 phần 2 câu c; căn 4-x2 có nghĩa ↔(2-x)(2+x) lớn hơn hoặc bằng 0 ↔x<=2 hoặc x >= -2 câu d;căn x2-1 có nghĩa ↔(x-1)(x+1)>=0↔x>=1 hoặc x>=-1

Bài 2:
c: Ta có: \(3x-\sqrt{x-1}=5\)
\(\Leftrightarrow\sqrt{x-1}=3x-5\)
\(\Leftrightarrow9x^2-30x+25-x+1=0\)
\(\Leftrightarrow9x^2-31x+26=0\)
\(\text{Δ}=\left(-31\right)^2-4\cdot9\cdot26=25\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{31-5}{18}=\dfrac{13}{9}\\x_2=\dfrac{31+5}{18}=2\end{matrix}\right.\)

\(\Delta'=16-\left(3m+1\right)\ge0\Rightarrow m\le5\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-8\\x_1x_2=3m+1\end{matrix}\right.\)
Kết hợp điều kiện đề bài ta được: \(\left\{{}\begin{matrix}x_1+x_2=-8\\5x_1-x_2=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-8\\6x_1=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-1\\x_2=-7\end{matrix}\right.\)
Thế vào \(x_1x_2=3m+1\)
\(\Rightarrow\left(-1\right).\left(-7\right)=3m+1\)
\(\Rightarrow m=2\) (thỏa mãn)

`a)\sqrt{16x+48}+\sqrt{x+3}=15` `ĐK: x >= -3`
`<=>4\sqrt{x+3}+\sqrt{x+3}=15`
`<=>5\sqrt{x+3}=15`
`<=>\sqrt{x+3}=3`
`<=>x+3=9<=>x=6` (t/m).
`b)\sqrt{x^2-4}-3\sqrt{x-2}=0` `ĐK: x >= 2`
`<=>\sqrt{x-2}(\sqrt{x+2}-3)=0`
`<=>[(\sqrt{x-2}=0),(\sqrt{x+2}=3):}`
`<=>[(x-2=0),(x+2=9):}<=>[(x=2(t//m)),(x=7(t//m)):}`

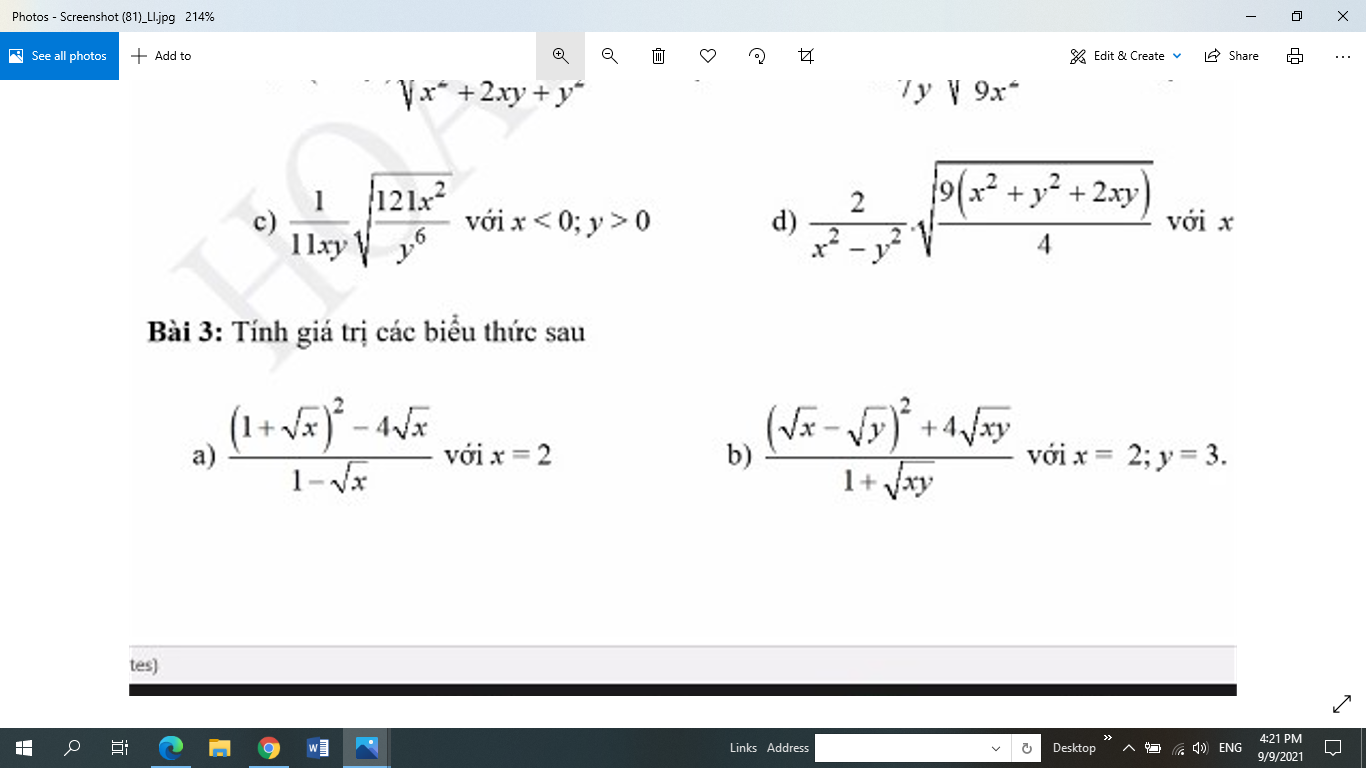
\(3,\\ a,\dfrac{\left(1+\sqrt{x}\right)^2-4\sqrt{x}}{1-\sqrt{x}}\\ =\dfrac{\sqrt{x}-2\sqrt{x}+1}{1-\sqrt{x}}=\dfrac{\left(1-\sqrt{x}\right)^2}{1-\sqrt{x}}=1-\sqrt{x}=1-\sqrt{2}\)
\(b,\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{1+\sqrt{xy}}\\ =\dfrac{x+2\sqrt{xy}+y}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{1+\sqrt{xy}}\\ =\dfrac{\left(\sqrt{2}+\sqrt{3}\right)^2}{1+\sqrt{6}}=\dfrac{5+2\sqrt{6}}{1+\sqrt{6}}\\ =\dfrac{\left(5+2\sqrt{6}\right)\left(\sqrt{6}-1\right)}{5}\\ =\dfrac{3\sqrt{6}+7}{5}\)

Bài 3:
\(a,=\sqrt[3]{\left(x-1\right)^3}-\sqrt[3]{\left(5x+1\right)^3}=x-1-5x-1=-4x-2\\ b,=6a-6a+20a=20a\)
Bài 2:
\(a,=2\sqrt[3]{6}+3\sqrt[3]{5}-4\sqrt[3]{6}-2\sqrt[3]{5}=\sqrt[3]{5}-2\sqrt[3]{6}\\ b,=\sqrt[3]{8}-4\sqrt[3]{27}+2\sqrt[3]{64}=2-12+16=6\\ c,=\sqrt[3]{64}+\sqrt[3]{48}+\sqrt[3]{36}-\sqrt[3]{48}-\sqrt[3]{36}-\sqrt[3]{27}=4-3=1\\ d,=\sqrt[3]{162\left(-2\right)\cdot\dfrac{2}{3}}=\sqrt[3]{-216}=-6\)

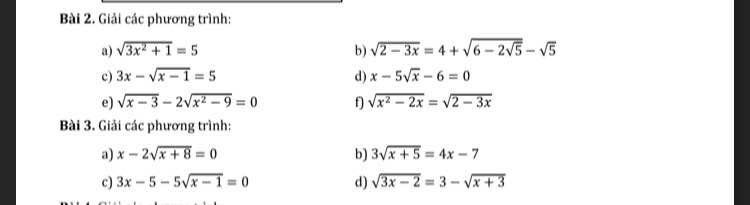


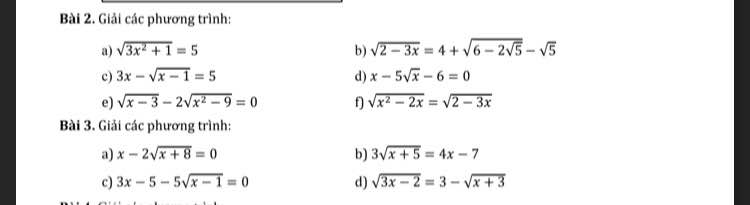



Bài 1:
Gọi chiều dài là x(Điều kiện: x>10,5)
Chiều rộng là 21-x
Theo đề, ta có: \(x^2+\left(21-x\right)^2=225\)
\(\Leftrightarrow x^2+x^2-42x+441-225=0\)
\(\Leftrightarrow2x^2-42x+216=0\)
\(\Leftrightarrow x^2-21x+108=0\)
\(\Leftrightarrow\left(x-12\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\left(nhận\right)\\x=9\left(loại\right)\end{matrix}\right.\)
vậy: Chiều dài là 12m
Chiều rộng là 9m