DP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
0
O
1
9 tháng 10 2021
Bài 1:
a) \(=\dfrac{\sqrt{5}.\sqrt{7}}{5}=\dfrac{\sqrt{35}}{5}\)
b) \(=\dfrac{\left|y\right|}{\sqrt{3}}=\dfrac{\sqrt{3}y}{3}\)
c) \(=\dfrac{\sqrt{2}}{\sqrt{t}}=\dfrac{\sqrt{2t}}{t}\)
d) \(=\sqrt{\dfrac{7p^2-3p^2}{7}}=\sqrt{\dfrac{4p^2}{7}}=\dfrac{2\left|p\right|}{\sqrt{7}}=\dfrac{-2\sqrt{7}p}{7}\)
Bài 2:
a) \(=\dfrac{\sqrt{21}-\sqrt{15}}{3}\)
b) \(=\dfrac{10\left(4+3\sqrt{2}\right)}{16-18}=-20-15\sqrt{2}\)
c) \(=\dfrac{\left(3\sqrt{10}-5\right)\left(6+\sqrt{10}\right)}{36-10}=\dfrac{18\sqrt{10}+30-30-5\sqrt{10}}{26}=\dfrac{13\sqrt{10}}{26}=\dfrac{\sqrt{10}}{2}\)
HT
0
PM
1
27 tháng 8 2021
a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)
T
1
SA
14 tháng 6 2021
\(A=\dfrac{4x+2\sqrt{x}+2}{2\sqrt{x}+1}=\dfrac{2\sqrt{x}\left(2\sqrt{x}+1\right)+2}{2\sqrt{x}+1}=2\sqrt{x}+\dfrac{2}{2\sqrt{x}+1}\)
\(=2\sqrt{x}+1+\dfrac{2}{2\sqrt{x}+1}-1\ge2\sqrt{\left(2\sqrt{x}+1\right)\cdot\dfrac{2}{2\sqrt{x}+1}}-1=2\sqrt{2}-1\)
=> A \(\ge2\sqrt{2}-1\)
Dấu "=" xảy ra <=> \(2\sqrt{x}+1=\dfrac{2}{2\sqrt{x}+1}\)
<=> \(\left(2\sqrt{x}+1\right)^2=2\) <=> \(\left[{}\begin{matrix}2\sqrt{x}+1=2\\2\sqrt{x}+1=-2\left(loại\right)\end{matrix}\right.\)
<=> \(\sqrt{x}=\dfrac{1}{2}\) <=> \(x=\dfrac{1}{4}\)(tm)
Vậy minA = \(2\sqrt{2}-1\) khi x = 1/4
LN
1
6 tháng 7 2016
\(x^2+x^4-8^2+16\)
\(=x^{2+4}-8^2+4^2\)
\(=x^6-64+16\)
\(=x^2-48\)
\(=\left(x-\sqrt{48}\right)\left(x+\sqrt{48}\right)\)
TT
1
25 tháng 5 2021
`A=1/(x+sqrtx)+(2sqrtx)/(x-1)-1/(x-sqrtx)`
`=(sqrtx-1+2x-sqrtx-1)/(sqrtx(x-1))`
`=(2x-2)/(sqrtx(x-1))`
`=2/sqrtx`
`b)A=1`
`<=>2/sqrtx=1`
`<=>sqrtx=2`
`<=>x=4(tm)`
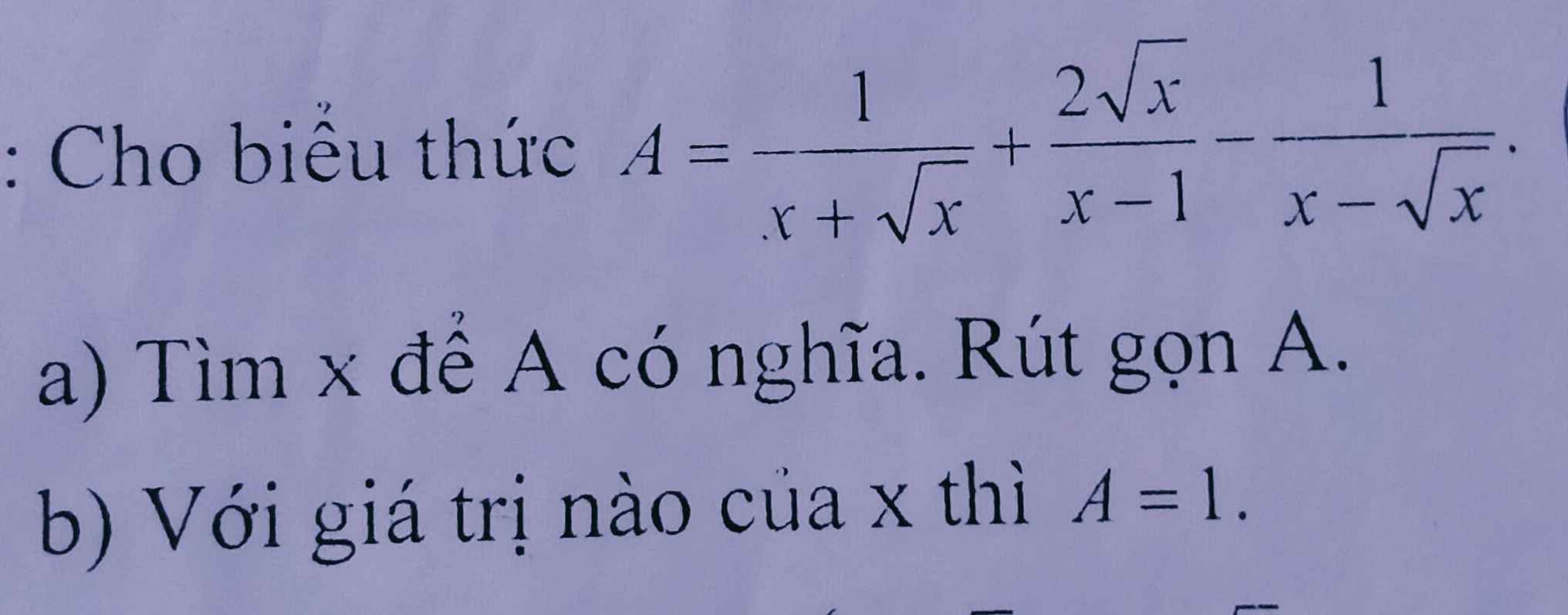
A B C D
Ta có :
\(\hept{\begin{cases}AC^2=AD^2+DC^2\\BD^2=AD^2+AB^2\end{cases}}\) vì \(CD>AB\Rightarrow AC>BD\)
b. ta có \(AC^2-BD^2=\left(AD^2+DC^2\right)-\left(AD^2+AB^2\right)=CD^2-AB^2\)