Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Cho hình bình hành ABCD
Xét tứ giác DBEC có
BE//DC
BE=DC
DO đó: DBEC là hình bình hành
Suy ra: DB//CE và DB=CE
Xét tứ giác BDFC có
BC//DF
BC=DF
Do đó: BDFC là hình bình hành
Suy ra: BD//CF và BD=CF
Ta có: BD//CF
BD//CE
CF và CE có điểm chung là C
Do đó: F,C,E thẳng hàng
mà CE=CF(=BD)
nên C la trung điểm của FE
hay F và E đối xứng nhau qua C

Trong sách có mà bạn ( Ít nhất cũng thuộc chứ )
1. Bình phương của một tổng:
\(\left(a+b\right)^2=a^2+2ab+b^2\)
2. Bình phương của một hiệu:
\(\left(a-b\right)^2=a^2-2ab+b^2\)
3. Hiệu hai bình phương:
\(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
4. Lập phương của một tổng:
\(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
5. Lập phương của một hiệu:
\(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
6. Tổng hai lập phương:
\(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)^3-3a^2b-3ab^2=\left(a+b\right)^3-3ab\left(a+b\right)\)
7. Hiệu hai lập phương:
\(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)^3+3a^2b-3ab^2=\left(a-b\right)^3+3ab\left(a-b\right)\)
Hok tốt

a:
b: TH1: \(\hat{BAD}>90^0;\hat{ABD}>90^0\)
Ta có: ABCD là hình thang
=>\(\hat{ABC}+\hat{BCD}=180^0\)
=>\(\hat{BCD}<180^0-90^0=90^0\)
=>\(\hat{BCD}<\hat{BAD}\)
TH2: \(\hat{ADC}>90^0;\hat{DCB}>90^0\)
Ta có: ABCD là hình thang
DC//AB
=>\(\hat{CDA}+\hat{DAB}=180^0\)
=>\(\hat{DAB}<180^0-90^0=90^0\)
=>\(\hat{DAB}<\hat{DCB}\)
c: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành

a) \(x^2-6x+3\)
\(=x^2-2.x.3+9-6\)
\(=\left(x-3\right)^2-\left(\sqrt{6}\right)^2\)
\(=\left(x-3-\sqrt{6}\right)\left(x-3+\sqrt{6}\right)\)
b) \(9x^2+6x-8\)
\(=\left(3x\right)^2+2.3x+1-9\)
\(=\left(3x+1\right)^2-3^2\)
\(=\left(3x+1-3\right)\left(3x+1+3\right)\)
\(=\left(3x-2\right)\left(3x+4\right)\)
d) \(x^3+6x^2+11x+6\)
\(=x^3+3x^2+3x^2+9x+2x+6\)
\(=x^2\left(x+3\right)+3x\left(x+3\right)+2\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2+3x+2\right)\)
\(=\left(x+3\right)\left(x^2+x+2x+2\right)\)
\(=\left(x+3\right)\left[x\left(x+1\right)+2\left(x+1\right)\right]\)
\(=\left(x+3\right)\left(x+1\right)\left(x+2\right)\)
e) \(x^3+4x^2-29x+24\)
\(=x^3+8x^2-4x^2-32x+3x+24\)
\(=x^2\left(x+8\right)-4x\left(x+8\right)+3\left(x+8\right)\)
\(=\left(x+8\right)\left(x^2-4x+3\right)\)
\(=\left(x+8\right)\left(x^2-3x-x+3\right)\)
\(=\left(x+8\right)\left[x\left(x-3\right)-\left(x-3\right)\right]\)
\(=\left(x+8\right)\left(x-3\right)\left(x-1\right)\)
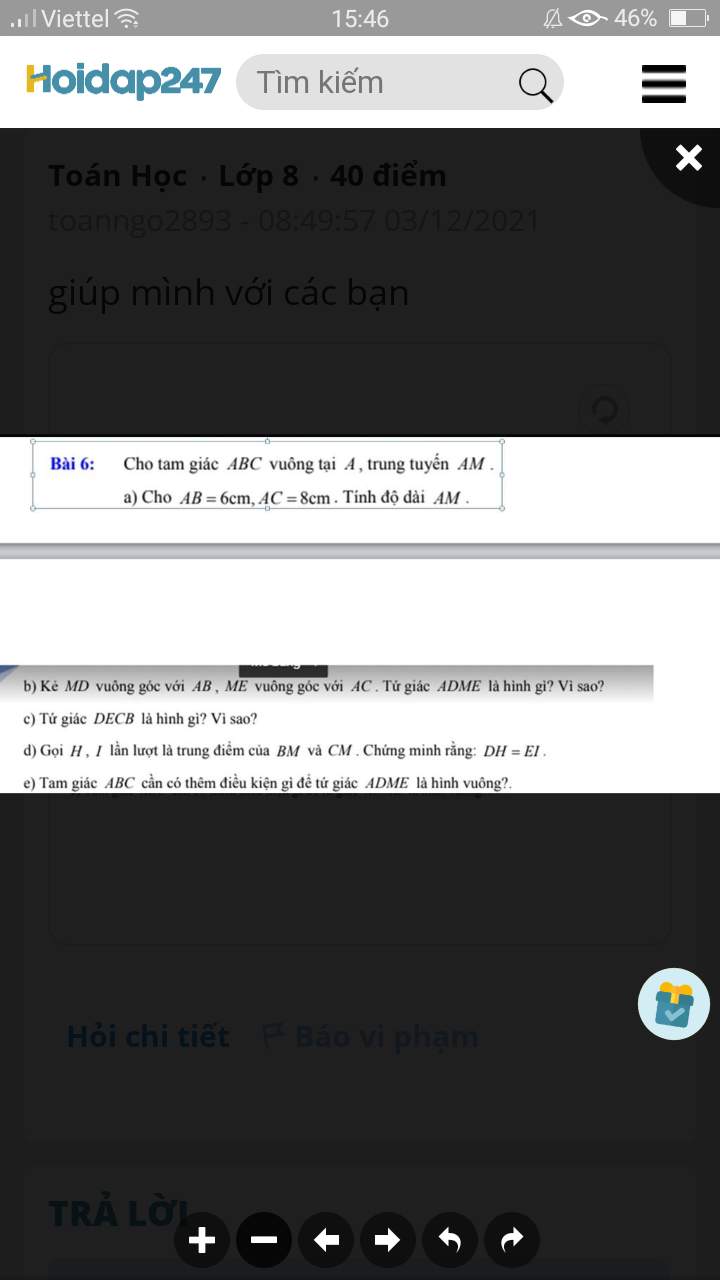



b: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó: ADME là hình chữ nhật
Mình cần phần d,e ạ