
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)


a) \(A=x^4+4x+7=\left(x^2+4x+4\right)+3=\left(x+2\right)^2+3\ge3\)
\(minA=3\Leftrightarrow x=-2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxC=7\Leftrightarrow x=2\)
d) \(D=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxD=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)

\(d,\left(2x-1\right)\left(x+3\right)+2x\left(2-x\right)=10-8\left(x+4\right)\\ \Leftrightarrow2x^2+6x-x-3+4x-2x^2=10-8x-32\\ \Leftrightarrow17x=19\Leftrightarrow x=\dfrac{19}{17}\)
vậy phương trình đã cho có nhiệm \(x=\dfrac{19}{17}\)
Ta có: \(\left(2x-1\right)\left(x+3\right)+2x\left(2-x\right)=10-8\left(x+4\right)\)
\(\Leftrightarrow2x^2+6x-x-3+4x-2x^2=-8x-22\)
\(\Leftrightarrow18x=-19\)
hay \(x=-\dfrac{19}{18}\)

Lời giải:
a. $(x^2-1)(x^2+2x)=x^4+2x^3-x^2-2x$
b. $(2x-1)(3x+2)(3-x)=(6x^2+4x-3x-2)(3-x)$
$=(6x^2+x-2)(3-x)=18x^2-6x^3+3x-x^2-6+2x$
$=-6x^3+17x^2+5x-6$
c.
$(x+3)(x^2+3x-5)=x^3+3x^2-5x+3x^2+9x-15$
$=x^3+6x^2+4x-15$
d.
$(x+1)(x^2-x+1)=x^3+1^3=x^3+1$
e.
$(2x^3-3x-1)(5x+2)=10x^4+4x^3-15x^2-6x-5x-2$
$=10x^4+4x^3-15x^2-11x-2$
f.
$(x^2-2x+3)(x-4)=x^3-4x^2-2x^2+8x+3x-12$
$=x^3-6x^2+11x-12$

Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A


\(a,\dfrac{13z}{63x^2y^3}=\dfrac{65z^3}{315x^2y^3z^2};\dfrac{-y}{15xz^2}=\dfrac{-21xy^4}{315x^2y^3z^2};\dfrac{2x}{9y^2z}=\dfrac{70x^3yz}{315x^2y^3z}\\ b,\dfrac{x}{x-y}=\dfrac{-x\left(y-x\right)^2}{\left(y-x\right)^3};\dfrac{y}{\left(x-y\right)^2}=\dfrac{y}{\left(y-x\right)^2}=\dfrac{y}{\left(y-x\right)^3}\\ c,\dfrac{1}{2x+4}=\dfrac{x-2}{2\left(x+2\right)\left(x-2\right)};\dfrac{x}{2x-4}=\dfrac{x\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)};\dfrac{3}{4-x^2}=-\dfrac{6}{2\left(x-2\right)\left(x+2\right)}\)
 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn giúp em bài này vs ạ em cảm ơn trc ạ
giúp em bài này vs ạ em cảm ơn trc ạ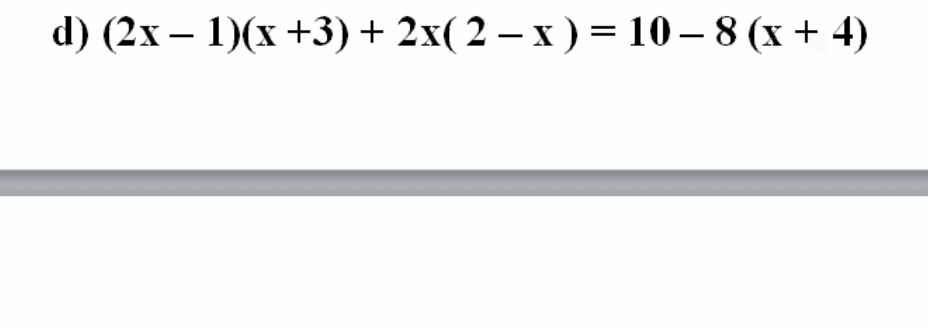 Giúp em vs ạ ! Em camon.
Giúp em vs ạ ! Em camon. 




\(< =>\left(a+b\right)^2+2\left(a+b\right)c+c^2-3ab-3bc-3ca=0\)
\(< =>a^2+2ab+b^2+2ac+2bc-3ab-3bc-3ca=0\)
\(< =>a^2+b^2+c^2-ab-bc-ca=0\)
\(< =>2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(< =>a^2-2ab+b^2+a^2-2ac+c^2+b^2-2bc+c^2=0\)
\(< =>\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2=0\)
dấu"=" xảy ra<=>a=b=c
Ta có :
\(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)-3\left(ab+bc+ac\right)=0\)
\(\Leftrightarrow a^2+b^2+c^2+ab+bc+ac=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2+2ab+2bc+2ac=0\)(nhân 2 vế cho 2)
\(\Leftrightarrow\)\(a^2+b^2+c^2+\left(a+b\right)^2+\left(b+c\right)^2+\left(a+c\right)^2=0\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}a^2=0,b^2=0,c^2=0\\\left(a+b\right)^2=0\\\left(b+c\right)^2=0\\\left(a+c\right)^2=0\end{matrix}\right.\Leftrightarrow a=b=c=0\left(đcpcm\right)\)