Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ đề bài, ta có hình vẽ sau:
\(\hat{BAC}=\hat{BAH}+\hat{CAH}=10^0+10^0=20^0\)
Xét ΔABC có
AH là đường cao
AH là đường phân giác
Do đó: ΔABC cân tại A
=>\(\hat{ABC}=\frac{180^0-\hat{BAC}}{2}=\frac{180^0-20^0}{2}=80^0\)
Ta có: \(\hat{KBC}+\hat{KBA}=\hat{ABC}\) (tia BK nằm giữa hai tia BA và BC)
=>\(\hat{KBA}=80^0-40^0=40^0\)
Xét ΔABG và ΔACG có
AB=AC
\(\hat{BAG}=\hat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG
=>\(\hat{ABG}=\hat{ACG}\)
=>\(x=40^0\)


\(A=\left(2n-1\right)^3-2n+1\)
\(A=8n^3-6n+6n-1-2n+1\)
\(A=8n^3-2n=2n\left(4n^2-1\right)\)
\(A=2n\left(2n+1\right)\left(2n-1\right)\)
\(A=\left(2n-1\right)2n\left(2n+1\right)⋮6\) ( 3 số tự nhiên liên tiếp)

Xét tứ giác ANHM có \(\widehat{ANH}+\widehat{AMH}=180^0\)
nên AHNM là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác AHNM
Xét (O) có
\(\widehat{ANM}\) là góc nội tiếp chắn cung AM
\(\widehat{AHM}\) là góc nội tiếp chắn cung AM
Do đó: \(\widehat{ANM}=\widehat{AHM}\)
mà \(\widehat{AHM}=\widehat{B}\)
nên \(\widehat{ANM}=\widehat{B}\)
Gọi K là giao điểm của AD và NM
Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên DA=DC
=>ΔDAC cân tại D
=>\(\widehat{C}=\widehat{DAC}\)
\(\widehat{KAN}+\widehat{KNA}=\widehat{B}+\widehat{C}=90^0\)
nên \(\widehat{AKN}=90^0\)
=>AD\(\perp\)NM

Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

a) x(x-y)+(x-y)=(x+1)(x-y)
b) 2x+2y -x(x+y)= 2(x+y)-x(x+y)=(2-x)(x+y)
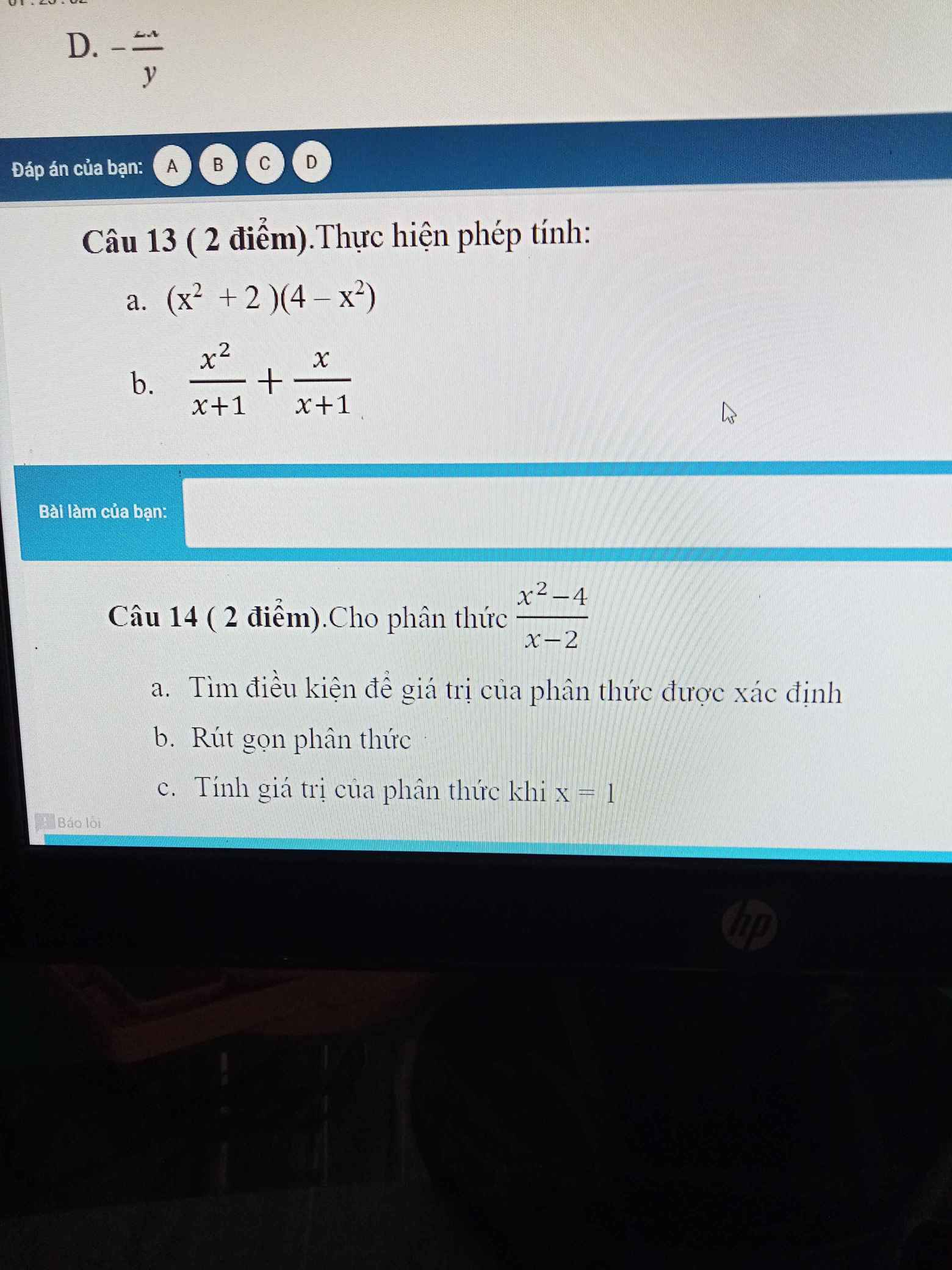


 mọi người giải giúp em với ạ em đang cần gấp lắm ạ
mọi người giải giúp em với ạ em đang cần gấp lắm ạ 
 _ mọi người giúp em với ạ! Em đang cần gấp ạ_
_ mọi người giúp em với ạ! Em đang cần gấp ạ_


Câu 14;
a: ĐKXĐ: x<>2
b: \(\dfrac{x^2-4}{x-2}=x+2\)
c: Thay x=1 vào x+2, ta được:
x+2=1+2=3