
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5

Ta có:
Cy // mn
=>ACy + A2=180 độ (2 góc trong cùng phía)
=>A2=180 độ - ACy=180 độ - 130 độ=50 độ
Lại có:
Bx // mn
=>ABx + A1=180 độ (2 góc trong cùng phía)
=>A1=180 độ - ABx=180 độ - 110 độ=70 độ
Mà A1 + BAC + A2=180 độ (Các góc kề bù)
=>BAC=180 độ - A1 - A2=180 độ - 70 độ - 50 độ=60 độ


3.15:
EF vuông góc MH
NP vuông góc MH
Do đó: EF//NP
3.17:
góc yKH+góc H=180 độ
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ky//Hx

Gọi chiều dài là a(m)
=> Chiều dài là \(\dfrac{5400}{a}\left(m\right)\)
Theo đề bài ta có: \(\dfrac{5400}{a}:a=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{5400}{a^2}=\dfrac{3}{2}\)
\(\Rightarrow a^2=3600\Rightarrow a=60\left(m\right)\)
Vậy chiều rộng là 60m, chiều dài là \(\dfrac{5400}{a}=\dfrac{5400}{60}=90\left(m\right)\)
Chu vi hình chữ nhật là: \(\left(90+60\right).2=300\left(m\right)\)

a) Xét ∆ ABM(<A=90°(gt)) và ∆NDM(<N=90°(gt)), ta có:
<BMA=<DMN( đối đỉnh)
BM=DM(gt)
⟹∆ABM=∆NDM(c.h=g.n)
b) Ta có:
<ABM=<MDN(Vì ∆ABM=∆NDM(CM ở a))
mà <ABM=<CBM(gt)
⟹<MDN=<CBM
⟹∆EBD cân tại E
⟹ BE=DE
c)Áp dụng định lý Py-ta-go vào ∆ABC(<A=90°(gt)), ta có:
BC2=AB2+AC2
⟹AB2=BC2-AC2=152-122=225-144=81
⟹AB=√81=9cm
mà AB=DN(Vì ∆ABM=∆NDM(CM ở a))
⟹AB=DN=9cm
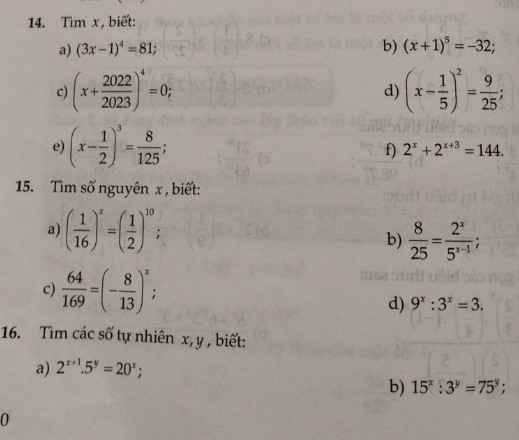


 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ

 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ mn giúp em bài 9 với ạ! Em cảm ơn nhiều :3
mn giúp em bài 9 với ạ! Em cảm ơn nhiều :3
14:
a) \(\left(3x-1\right)^4=81\)
\(\Rightarrow\left(3x-1\right)^4=\left(\pm3\right)^4\)
\(\Rightarrow\left[{}\begin{matrix}3x-1=3\\3x-1=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3x=4\\3x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
b) \(\left(x+1\right)^5=-32\)
\(\Rightarrow\left(x+1\right)^5=\left(-2\right)^5\)
\(\Rightarrow x+1=-2\)
\(\Rightarrow x=-3\)
c) \(\left(x+\dfrac{2022}{2023}\right)^3=0\)
\(\Rightarrow x+\dfrac{2022}{2023}=0\)
\(\Rightarrow x=-\dfrac{2022}{2023}\)
d) \(\left(x-\dfrac{1}{5}\right)^2=\dfrac{9}{25}\)
\(\Rightarrow\left(x-\dfrac{1}{5}\right)^2=\left(\dfrac{3}{5}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{5}=\dfrac{3}{5}\\x-\dfrac{1}{5}=-\dfrac{3}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{2}{5}\end{matrix}\right.\)
e) \(\left(x-\dfrac{1}{2}\right)^3=\dfrac{8}{125}\)
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{2}{5}\right)^3\)
\(\Rightarrow x-\dfrac{1}{2}=\dfrac{2}{5}\)
\(\Rightarrow x=\dfrac{9}{10}\)
f) \(2^x+2^{x+3}=144\)
\(\Rightarrow2^x\cdot\left(1+2^3\right)=144\)
\(\Rightarrow2^x\cdot9=144\)
\(\Rightarrow2^x=16\)
\(\Rightarrow2^x=2^4\)
\(\Rightarrow x=4\)
16:
a: \(\Leftrightarrow2^{x+1}\cdot5^y=\left(2^2\cdot5\right)^x=2^{2x}\cdot5^x\)
=>2x=x+1 và x=y
=>x=1=y
b: \(\Leftrightarrow5^x\cdot3^{x-y}=3^y\cdot5^{2y}\)
=>x=2y và x-y=y
=>x=2y(luôn đúng)
Vậy: \(\left(x,y\right)\in N\)