Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác OBA có OB = OC = BC = R
Vậy tam giác OAB là tam giác đều
=> ^BOC = ^OBC = ^OCB = 600
Vì AB ; AC là tiếp tuyến đường tròn (O) với B;C là tiếp điểm
=> ^OBA = ^OCA = 900
=> ^ABC = ^OBA - ^OBC = 900 - 600 = 300
Do AB = AC ( tc tiếp tuyến cắt nhau )
=> ^ABC = ^ACB = 300
=> ^BAC = 1800 - 2^ABC = 1200

a. Ta có góc BOC = 120\(^0\)
\(\Rightarrow\) góc BAC = 60\(^0\). Vì AB và AC là tiếp tuyến nên AB = AC.
Do đó, tam giác ABC là tam giác đều.
Vì tam giác ABC đều nên ta có BC = AB = AC = 2R.
b. Ta có góc BOC = 120\(^0\), suy ra góc BAC = 60\(^0\).
Gọi H là hình chiếu của O trên BC. Khi đó OH = R.cos60\(^0\) = R/2.
Gọi x = BM, y = MC. Ta có:
+ BH = R-X
+ CH = R-Y
+ AH = AB - BH = R + x
+ AH = AC - CH = R + y
Áp dụng định lý Ptolemy cho tứ giác a. Ta có góc BOC = 120\(^0\), suy ra góc BAC = 60\(^0\). Vì AB và AC là tiếp tuyến nên AB = AC. Do đó, tam giác ABC là tam giác đều.
Vì tam giác ABC đều nên ta có BC = AB = AC = 2R.
Áp dụng định lý Ptolemy cho tứ giác ABOM và ACOM, ta có:
AB . OM + AC . OM = AO . BC
R . (x + y) + R . (x + y + BC) = AO . BC
R . (2x + 2y + BC) = AO . BC
Do đó, ta có: BC = (2R . x)/(AO - 2R) = (2R . y)/(AO - 2R)
Gọi T là điểm cắt của tiếp tuyến tại M với BC. Ta có:
+ OT vuông góc với BC
+ MT là đường trung bình của tam giác OBC
Do đó, ta có: MT = (1/2)BC = R . x/(AO - 2R) = R . y/(AO - 2R)
Gọi G là trọng tâm của tam giác AEF. Ta có:
+ OG song song với EF và bằng một nửa đường cao AH của tam giác ABC
+ AG = (2/3)AH
Do đó, ta có: OG = (1/3)AO và EF = 20G = (2/3)AO/3
Áp dụng định lý Ptolemy cho tứ giác OFCI, ta có:
OF . IC + OI . FC = OC . FI
R . (y + EF) + R . x = R . (y+x)
R . y + (2/3)AO/3 = R . x
Do đó, ta có: R.y/(AO-2R) + (2/3)AO/(3R) = R.x/(AO-2R)
Tổng quát hóa, ta có: nếu M thuộc cung BC nhỏ thì chu vi tam giác AEF không đổi.
Câu c. mik ko bt làm

Chọn đáp án A.

Góc 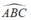 là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC nên:
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC nên:
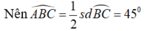

a: Xét (O) có
DB là tiếp tuyến
DC là tiếp tuyến
Do đó: DB=DC
hay D nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
hay OD⊥BC(3)
Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
hay AC⊥CB(4)
Từ (3) và (4) suy ra AC//OD

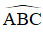 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC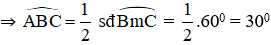
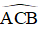 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB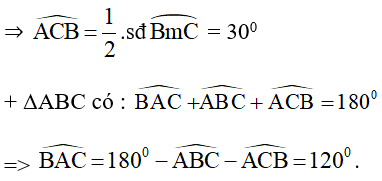

Gọi \(\left\{H\right\}=BC\cap OA\)
\(\left\{{}\begin{matrix}AB=AC\\OB=OC=R\end{matrix}\right.\Rightarrow OA\text{ là trung trực }BC\\ \Rightarrow\Delta OBC\text{ cân tại B}\\ \Rightarrow OH\text{ là trung tuyến}\)
\(\Rightarrow BH=HC=\dfrac{R\sqrt{3}}{2}\\ \Rightarrow\cos OBH=\dfrac{BH}{OB}=\dfrac{\dfrac{R\sqrt{3}}{2}}{R}=\dfrac{\sqrt{3}}{2}\\ \Rightarrow\widehat{OBH}=30^0\\ \Rightarrow\widehat{ABC}=\widehat{ABO}-\widehat{OBH}=60^0\\ \Rightarrow\Delta ABC\text{ đều}\\ \Rightarrow\widehat{ABC}=\widehat{ACB}=60^0\)