
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Dạng 1:
1/ ĐKXĐ: \(x\le0\)
2/ ĐKXĐ: \(x\ge\dfrac{3}{5}\)
3/ ĐKXĐ: \(x\le-4\)
4/ ĐKXĐ: \(x\ge5\)
Dạng 1:
\(1,ĐK:-2x+3\ge0\Leftrightarrow x\le\dfrac{3}{2}\\ 2,ĐK:5x-3\ge0\Leftrightarrow x\ge\dfrac{3}{5}\\ 3,ĐK:\dfrac{-100}{x+3}\ge0\Leftrightarrow x+3< 0\left(-100< 0;x+3\ne0\right)\\ \Leftrightarrow x< -3\\ 4,ĐK:\dfrac{x-5}{3}\ge0\Leftrightarrow x-5\ge0\left(3>0\right)\\ \Leftrightarrow x\ge5\)
Dạng 2:
\(1,=2\sqrt{5}-6\sqrt{5}+12\sqrt{5}-8\sqrt{5}=0\\ 9,=\left(3-\sqrt{5}\right)\left(\sqrt{5}-1\right)\sqrt{6+2\sqrt{5}}\\ =\left(3-\sqrt{5}\right)\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)\\ =4\left(3-\sqrt{5}\right)=12-4\sqrt{5}\\ 2,=\dfrac{4\sqrt{3}}{3}+15\sqrt{3}-3\sqrt{3}-\dfrac{20\sqrt{3}}{3}\\ =12\sqrt{3}-\dfrac{16\sqrt{3}}{3}=\dfrac{36\sqrt{3}-16\sqrt{3}}{3}=\dfrac{20\sqrt{3}}{3}\\ 10,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)


b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

1) Ta có: \(\sqrt{2x+5}=\sqrt{3-x}\)
\(\Leftrightarrow2x+5=3-x\)
\(\Leftrightarrow2x+x=3-5\)
\(\Leftrightarrow3x=-2\)
hay \(x=-\dfrac{2}{3}\)
2) Ta có: \(\sqrt{2x-5}=\sqrt{x-1}\)
\(\Leftrightarrow2x-5=x-1\)
\(\Leftrightarrow2x-x=-1+5\)
\(\Leftrightarrow x=4\)
3 , \(PT\left(đk:\frac{16}{3}\ge x\ge3\right)< =>x^2-3x=16-3x\)
\(< =>x^2-16=0< =>\left(x-4\right)\left(x+4\right)=0< =>\orbr{\begin{cases}x=4\left(tm\right)\\x=-4\left(ktm\right)\end{cases}}\)
4 , \(PT\left(đk:...\right)< =>2x^2-3=4x-3< =>2x^2-4x=0\)
\(< =>2x\left(x-2\right)=0< =>\orbr{\begin{cases}x=0\left(...\right)\\x=2\left(...\right)\end{cases}}\)
bạn tự tìm đk rồi đối chiếu nhé :P

1) Ta có: \(\sqrt{4x}=\sqrt{5}\)
nên 4x=5
hay \(x=\dfrac{5}{4}\)
2) Ta có: \(\sqrt{16x}=8\)
nên 16x=64
hay x=4
3, \(2\sqrt{x}=\sqrt{9x}-3\left(đk:x\ge0\right)\)
\(< =>2\sqrt{x}-3\sqrt{x}+3=0\)
\(< =>3-\sqrt{x}=0< =>x=9\)(tmđk)
4, \(\sqrt{3x-1}=4\left(đk:x\ge\frac{1}{3}\right)\)
\(< =>3x-1=16< =>3x-17=0\)
\(< =>x=\frac{17}{3}\)(tmđk)

a: \(2\sqrt{45}+\sqrt{5}-3\sqrt{80}\)
\(=6\sqrt{5}+\sqrt{5}-12\sqrt{5}\)
\(=-5\sqrt{5}\)

1) ĐKXĐ: \(x\ge0\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge4\)
4) ĐKXĐ: \(x>16\)
5) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge0\end{matrix}\right.\)
6) ĐKXĐ: \(\left[{}\begin{matrix}x\le-1\\x\ge4\end{matrix}\right.\)
7) ĐKXĐ: \(\left[{}\begin{matrix}1\le x\\x< 3\end{matrix}\right.\)
8) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x>3\end{matrix}\right.\)
9) ĐKXĐ: \(x\in R\)
10) ĐKXĐ: \(x\in R\)
11) ĐKXĐ: \(x\in R\)
12) ĐKXĐ: \(x\in R\)
13) ĐKXĐ: \(x\in R\)
14) ĐKXĐ: \(x\in R\)
15) ĐKXĐ: \(x\in R\)
16) ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
17) ĐKXĐ: \(x\ge7\)
18) ĐKXĐ: \(x\ge-5\)

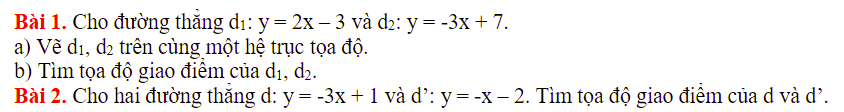
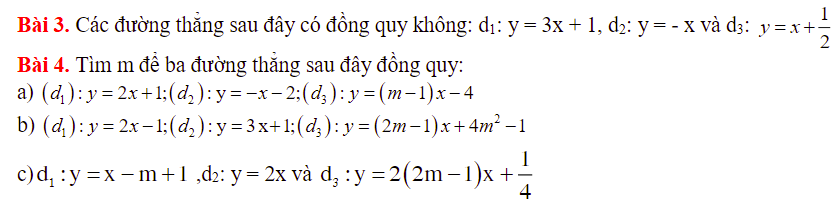
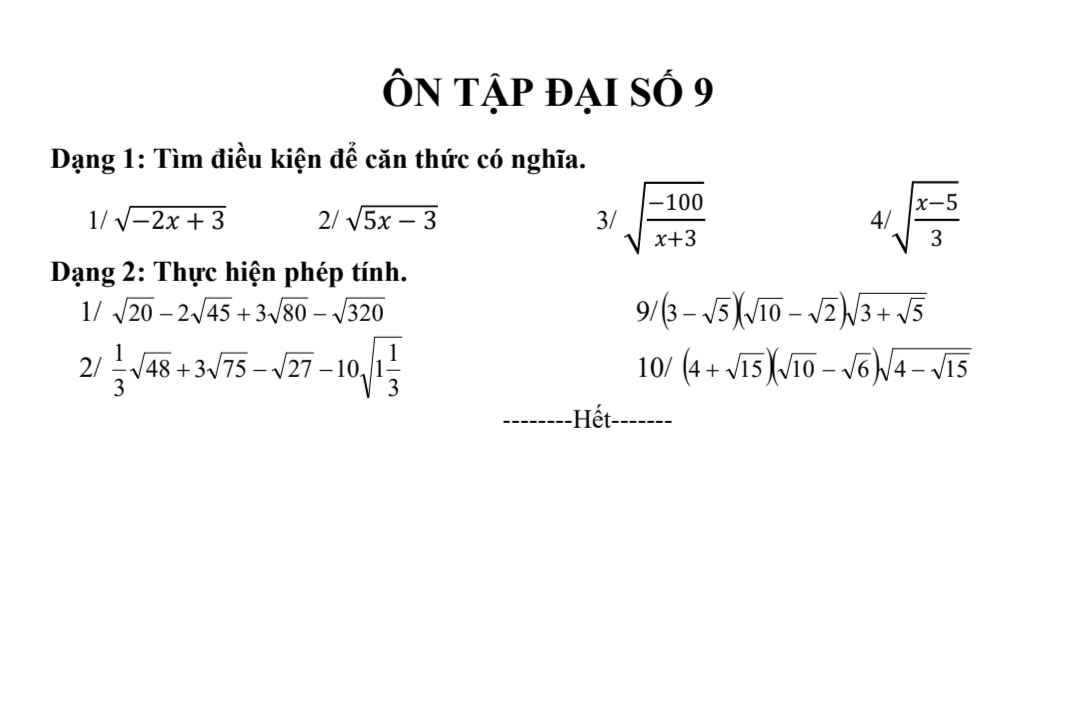

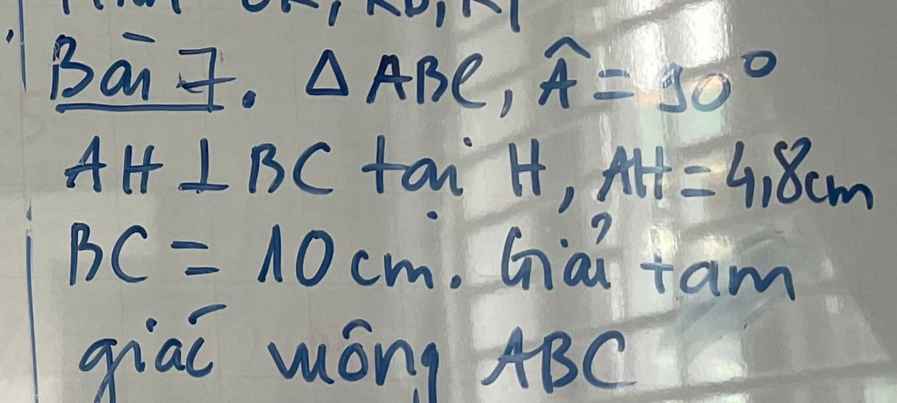
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp

