K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
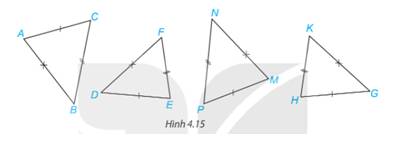
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)
S
subjects
CTVHS
28 tháng 8
bài 2: a. ta có góc ADE = góc ABC (= 45 độ)
mà 2 góc này ở vị trí đồng vị
⇒ DE // BC
b. ta có góc FEC = góc ECB
mà 2 góc này ở vị trí so le trong
⇒ EF // BC
c. vì DE // BC và EF // BC nên DE ≡ EF
⇒ 3 điểm D,E,F thẳng hàng
bài 3:
a. ta có góc CHK = góc CAB = 90 độ
mà 2 góc này ở vị trí đồng vị
⇒ KH // AB
b. ta có góc IKB = góc KBA = 60 độ
mà 2 góc này ở vị trí so le trong
⇒ KI // AB
c. vì KH // AB và KI // AB nên KH ≡ KI
⇒ 3 điểm H,K,I thẳng hàng
QT
1
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
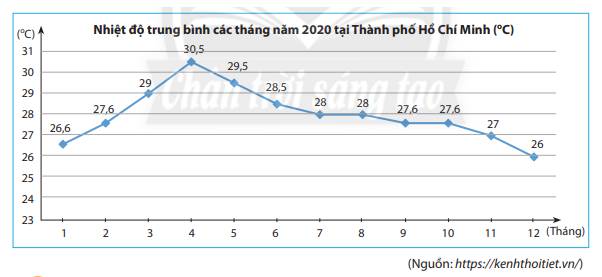
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
Lời giải:
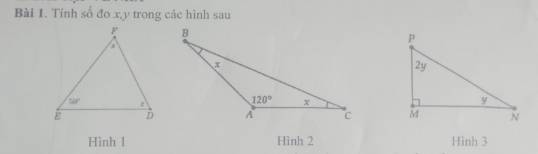
Áp dụng tính chất tổng 3 góc trong 1 tam giác bằng $180^0$
Hình 1: Hình không rõ ràng. Bạn xem lại.
Hình 2: $x+x+120^0=180^0$
$2x+120^0=180^0$
$2x=60^0$
$x=60^0:2=30^0$
Hình 3:
$2y+y+90^0=180^0$
$3y=180^0-90^0=90^0$
$y=90^0:3=30^0$
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 1 2024
Đổi 30 phút = 0,5 giờ
Quãng sông từ A đến B dài là:
\(x\) \(\times\) 0,5 + y \(\times\) 1 = 0,5\(x\) + y (km)
Kết luận Quãng đường từ A đên B dài: 0,5\(x\) + y (km)
3:
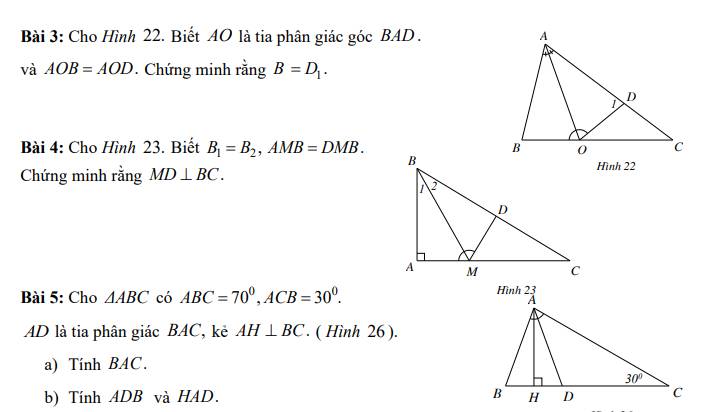
Xét ΔABO và ΔADO có
\(\widehat{AOB}=\widehat{AOD}\)
OA chung
\(\widehat{BAO}=\widehat{DAO}\)
Do đó: ΔABO=ΔADO
=>\(\widehat{ABO}=\widehat{ADO}\)(ĐPCM)
Bài 4:
Xét ΔBAM và ΔBDM có
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
\(\widehat{AMB}=\widehat{DMB}\)
Do đó: ΔBAM=ΔBDM
=>\(\widehat{BAM}=\widehat{BDM}=90^0\)
=>DM\(\perp\)BC
5:
a: Xét ΔBAC có
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=180^0-70^0-30^0=80^0\)
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{80^0}{2}=40^0\)
Xét ΔADC có góc ADB là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{C}=40^0+30^0=70^0\)
ΔAHD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}=90^0-70^0=20^0\)