
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1/
$C=5+(5^2+5^3)+(5^4+5^5)+.....+(5^{2022}+5^{2023})$
$=5+5^2(1+5)+5^4(1+5)+....+5^{2022}(1+5)$
$=5+(1+5)(5^2+5^4+....+5^{2022})$
$=5+6(5^2+5^4+....+5^{2022})$
$\Rightarrow C$ chia $6$ dư $5$
$\Rightarrow C\not\vdots 6$
2/
$D=(1+2+2^2)+(2^3+2^4+2^5)+....+(2^{2019}+2^{2020}+2^{2021})$
$=(1+2+2^2)+2^3(1+2+2^2)+....+2^{2019}(1+2+2^2)$
$=(1+2+2^2)(1+2^3+...+2^{2019})$
$=7(1+2^3+...+2^{2019})\vdots 7$
Ta có đpcm.

13.12 = 13.10 + 13.2 = 130 + 26 = 156
53.11 = 53.10 + 53 = 530 + 53 = 583
31.102 = 31.100 + 31.2 = 3100 + 62 = 3162
KL: a) = 156
b) b = 583
c) = 3162
\(13\times12=156\)
\(53\times11=583\)
\(31\times102=3162\)
học tốt


a: Ư(8)={1;2;4;8}
Ư(12)={1;2;3;4;6;12}
UC(8;12)={1;2;4}
b: B(16)={0;16;32;...}
B(24)={0;24;48;...}
BC(16,24)={0;48;96;...}



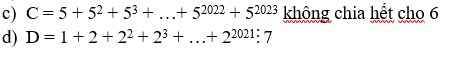
 giúp em với ạ em đang cần gấp cảm ơn ạ
giúp em với ạ em đang cần gấp cảm ơn ạ 
 Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.
Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.