
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



bài 12
điện trở tương đương của R2 và R3 là
R23=R2+R3=4+6=10(\(\Omega\))
điện trở tương đương của R4 và R5 là
R45=R4+R5=5+10=15(\(\Omega\))
điện trở tương đương của R23 và R45 là
\(\dfrac{1}{R2345}=\dfrac{1}{R23}+\dfrac{1}{R45}=\dfrac{1}{10}+\dfrac{1}{15}=\dfrac{1}{6}\)
\(\Rightarrow R2345=6\Omega\)
điện trở tương đương của R12345 là
R12345=R1+R2345=6+4=10(\(\Omega\))
điện trở tương đương của toàn mạch là
\(\dfrac{1}{Rtd}=\dfrac{1}{R12345}+\dfrac{1}{R6}=\dfrac{1}{10}+\dfrac{1}{10}=\dfrac{1}{5}\)
\(\Rightarrow Rtd=5\Omega\)
NHỚ TICK CHO MÌNH NHA CẢM ƠN
BÀI 13
gọi số điện trở của 2\(\Omega\)là x(x không âm và nguyên)
gọi số điện trở của 5\(\Omega\)là y(y không âm và nguyên)
ta có 2x+5y=30(vì đây là mạch nối tiếp)
\(\Rightarrow\)2x=30-5y
\(\Rightarrow\)x=15-\(\dfrac{5y}{2}\)
đặt y=2a\(\Rightarrow\)x=15-5a
vì x,y lớn hơn 0 và sộ nguyên nên
y=2a\(\ge\)0\(\Rightarrow\)a\(\ge\)0
x=15-5a\(\ge0\Rightarrow a\le3\)
\(\Rightarrow0\le a\le3\)
\(\Rightarrow a\in0,1,2,3\)
a 0 1 2 3
x 15 10 5 0
y 0 2 4 6 (kẻ bảng nha bạn)
vậy mắc 10 điện trở 2om và 2 điện trở 5om hoặc 5 điện trở 2om và 4 điện trở 5om thì mạch mắc nối tiếp có điên trở tương đương là 30om
nhớ tick cho mk nha cảm ơn

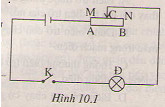
Trong sơ đồ mạch điện hình 4.1 sgk, các điện trở R1, R2 và ampe kế được mắc nối tiếp với nhau.

Trả lời:
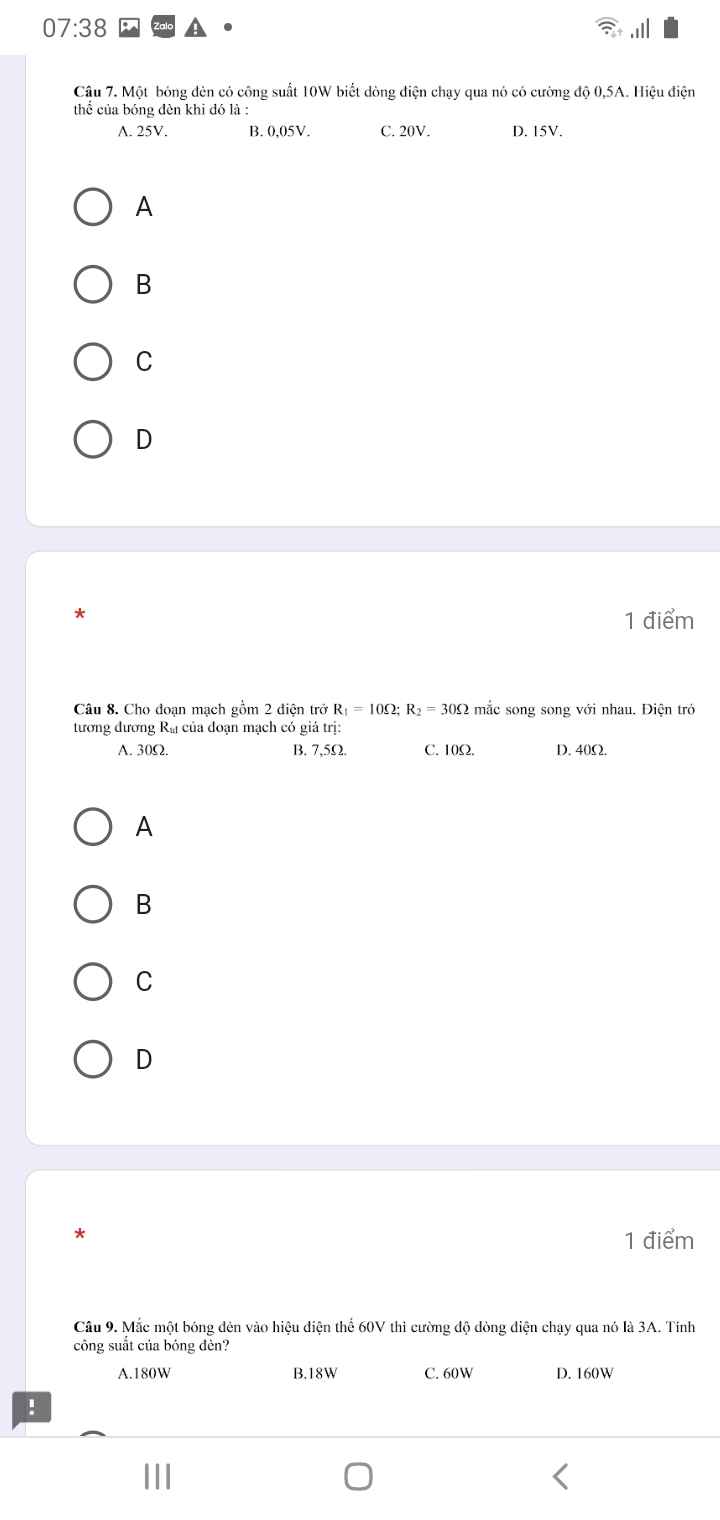
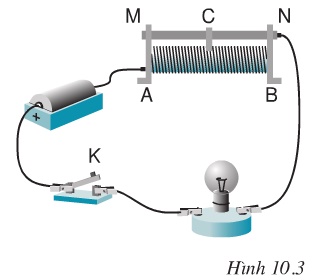
Hoạt động của biến trở có kí hiệu sơ đồ a, b, c trên hình 10.2 SGK : Khi dịch chuyển con chạy thì sẽ làm thay đổi chiều dài của phần cuộn dây có dòng điện chạy qua và do đó làm thay đổi ddiiejn trở của biện trở.

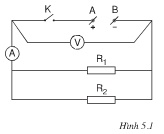
Trong sơ đồ mạch điện hình 5.1 sgk, các điện trở R1, R2 được mắc song song với nhau. Ampe kế dùng để đo cường độ dòng điện chạy trong mạch, vôn kế đo hiệu điện thé giữa hai đầu đoạn mạch.

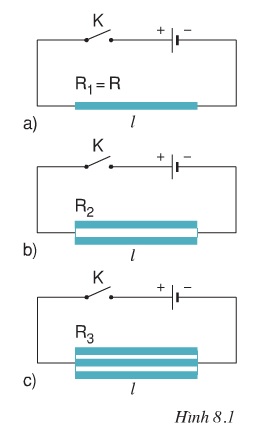
C3. Để xây dựng công thức tính điện trở R của một đoạn dây dẫn có chiều dài l, có tiết diện S và làm bằng vật liệu có điện trở suất p, hãy tính theo các bước như bảng 2.

Hướng dẫn.
R1 = p
R2 = p.l
R3 =


 mọi người ơi ai biết thì chỉ mình bài 12,13,14,15 với nha😩😩😩
mọi người ơi ai biết thì chỉ mình bài 12,13,14,15 với nha😩😩😩




 tick cho mình nha !!!
tick cho mình nha !!!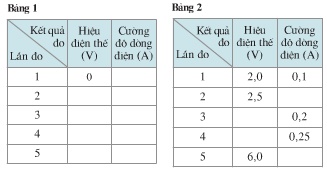
Câu 6:
\(U=I.R=10.1,5=15\left(V\right)\)
Câu 7:
\(P=U.I\Rightarrow U=\dfrac{P}{I}=\dfrac{10}{0,5}=20\left(V\right)\)
Câu 8:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{10.30}{10+30}=7,5\left(\Omega\right)\)