TD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 5 2017
a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.
, có môn gì cũng được mọi người ạ!!!
SG
1
15 tháng 4 2017
a) Bảng phân bố tần số (về tuổi thọ bóng đèn điện) có thể viết dưới dạng như sau:
Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:
.(3x1150 + 6x1160 + 12x1170 + 6x1180 + 3x1190)
= 1170.
b) Số trung bình về chiều dài lá cây dương xỉ trong bài tập 2 trong là:
.(8x15 + 18x25 + 24x35 + 10x45) = 31 (cm).
Q
29 tháng 5 2017
a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.
LT
3
AN
30 tháng 10 2017
Đường thẳng y = ax + b đi qua A( -1; 2) và B( 2; -3)
Nên có hpt: \(\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(y=-\dfrac{5}{3}x+\dfrac{1}{3}\)
-> Chon B
AN
30 tháng 10 2017
Câu 9: ĐKXĐ: \(3-2x\ge0\)
\(\Leftrightarrow x\le\dfrac{3}{2}\)
-> Chọn B
Câu 10: Bấm máy là ra.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
5.
Tọa độ dỉnh của (P) là: \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\Rightarrow I\left(1;-4m-2\right)\)
Để I thuộc \(y=3x-1\)
\(\Rightarrow-4m-2=3.1-1\)
\(\Rightarrow m=-1\)
6.a.
Với \(a\ne0\)
\(\left\{{}\begin{matrix}64a+8b+c=0\\-\dfrac{b}{2a}=5\\\dfrac{4ac-b^2}{4a}=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}64a+8b+c=0\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-64a-8b=-64a-8\left(-10a\right)=16a\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Rightarrow4a.16a-\left(-10a\right)^2=48a\)
\(\Rightarrow a=-\dfrac{4}{3}\Rightarrow b=\dfrac{40}{3}\Rightarrow c=-\dfrac{64}{3}\)
Hay pt (P): \(y=-\dfrac{4}{3}x^2+\dfrac{40}{3}x-\dfrac{64}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
b.
Thay tọa độ 3 điểm vào pt (P) ta được:
\(\left\{{}\begin{matrix}c=-1\\a+b+c=-1\\a-b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\)
Pt (P): \(y=x^2-x-1\)
c.
Do (P) đi qua 3 điểm có tọa độ (1;16); (-1;0); (5;0) nên ta có:
\(\left\{{}\begin{matrix}a+b+c=16\\a-b+c=0\\25a+5b+c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=8\\c=10\end{matrix}\right.\)
hay pt (P) có dạng: \(y=-2x^2+8x+10\)
mk đang cần gấp lắm
23 tháng 6 2017
Theo bài ra :
\(\left(x+5\right)\left(x^2-1\right)\left(3-x\right)>0\)
<=> \(\left(x+5\right)\left(x-1\right)\left(x+1\right)\left(3-x\right)>0\)
Đặt \(\left(x+5\right)\left(x-1\right)\left(x+1\right)\left(3-x\right)=A\)
Ta có bảng xét dấu :
| \(-\infty\) | -5 | -1 | 1 | 3 | \(+\infty\) | ||||
| (x+5) | - | 0 | + | + | + | + | |||
| x2-1 | + | + | 0 | - | 0 | + | + | ||
| 3-x | + | + | + | + | 0 | - | |||
| A | - (loại) | 0 (loại) | +(t.m) | 0(loại) | -(loại) | 0(loại) | +(t.m) | 0(loại) | -(loại) |
Từ bảng xét dấu trên suy ra :
\(A>0\Rightarrow\left[{}\begin{matrix}-5< x< -1\\1< x< 3\end{matrix}\right.\)
17 tháng 5 2017
a) Điểm số của xạ thủ A có : \(\overline{x}\approx8,3\) điểm ; \(s_1^2\approx1,6;s_1\approx1,27\) điểm
Điểm số của xạ thủ B có \(\overline{y}=8,4\) điểm, \(s_2^2\approx1,77;s_2\approx1,33\) điểm
b) \(\overline{x}\approx\overline{y}=8,4\) điểm; \(s_1^2< s_2^2\), như vậy mức độ phân tán của các điểm số (so với số trung bình) của xạ thủ A là bé hơn. Vì vậy trong lần tập bắn này xạ thủ A bắn chụm hơn.
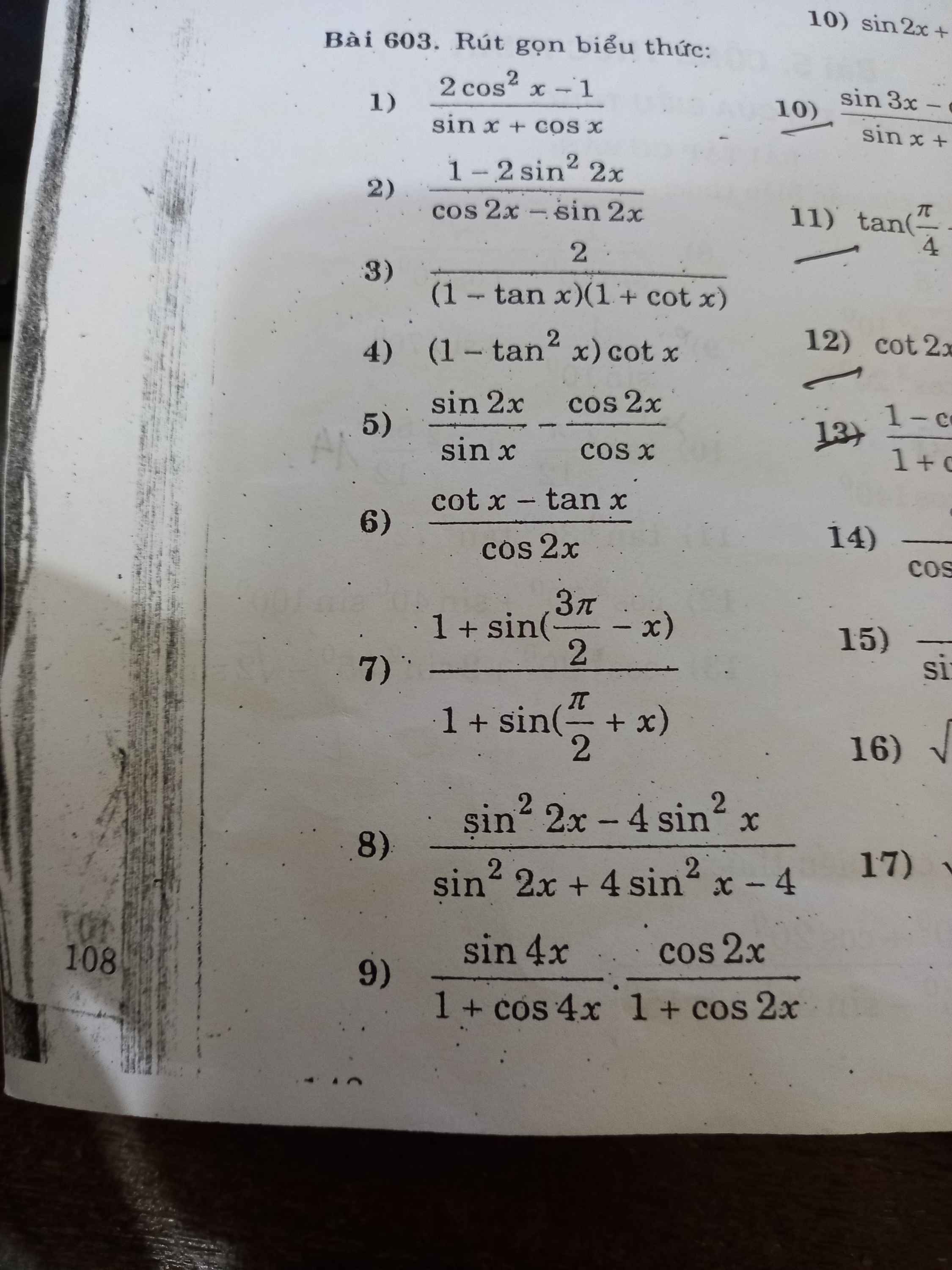
3:
\(=\dfrac{2}{1+cotx-tanx-1}=\dfrac{2}{cotx-tanx}\)
\(=2:\left(\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\right)=2:\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}\)
\(=\dfrac{sin2x}{cos2x}\)
=tan2x
4:
\(=\left(1-\dfrac{1}{cot^2x}\right)\cdot cotx=cotx-\dfrac{1}{cotx}=\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\)
\(=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}=\dfrac{cos2x}{\dfrac{1}{2}\cdot2\cdot sinx\cdot cosx}=\dfrac{cos2x}{sin2x}\cdot2\)
6:
\(=\dfrac{\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}}{cos2x}=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}:cos2x=\dfrac{1}{sinx\cdot cosx}\)