giúp em nhé mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 1
a: \(H=6x^3y^4-2x^4y^2+3x^2y^2+5x^4y^2-a\cdot x^3y^4\)
\(=\left(6x^3y^4-a\cdot x^3y^4\right)+3x^2y^2+3x^4y^2\)
\(=x^3y^4\left(6-a\right)+3x^2y^2+3x^4y^2\)
Để bậc của đa thức H bằng 6 thì 6-a=0
=>a=6
b: Khi a=6 thì \(H=3x^2y^2+3x^4y^2\)
\(=3x^2y^2\left(x^2+1\right)\)
Khi x<>0 và y<>0 thì \(x^2>0;y^2>0;x^2+1>1>0\)
=>\(x^2\cdot y^2\left(x^2+1\right)>0\)
=>\(H=3\cdot x^2y^2\left(x^2+1\right)>0\forall x,y\ne0\)
DH
5
N
24 tháng 11 2018
\(\left|x+2017\right|+\left|2018-x\right|\ge\left|x+2017+2018-x\right|=\left|4035\right|=4035\)
dấu = xảy ra khi và chỉ khi \(\left(x+2017\right).\left(2018-x\right)\ge0\)
\(\Rightarrow-2017\le x\le2018\)
Vậy min \(\left|x+2017\right|+\left|2018-x\right|\)=4035 khi \(-2017\le x\le2018\)
M
2
XO
17 tháng 8 2020
Ta có B = 5 + 52 + 53 + 54 + .... + 596
= (5 + 52) + (53 + 54) + .... + (595 + 596)
= 5(5 + 1) + 53(5 + 1) + ... + 595(5 + 1)
= (5 + 1)(5 + 53 + ... + 595)
= 6(5 + 53 + ... + 595)\(⋮6\)
b) Ta có B = 5 + 52 + 53 + 54 + 55 + 56 + .... 594 + 595 + 596
= (5 + 52 + 53) + (54 + 55 + 56) + .... + (594 + 595 + 596)
= 5(1 + 5 + 52) + 54(1 + 5 + 52) + .... + 594(1 + 5 + 52)
= (1 + 5 + 52)(5 + 54 + .... + 594)
= 31(5 + 54 + .... + 594)\(⋮31\)
c) B = 5 + 52 + 53 + 54 + .... + 595 + 596
= (5 + 53 + ... 593 + 595) + (52 + 54 + .... 594 + 596)
= [5(1 + 52) + ... + 593(1 + 52)] + [52(1 + 52) + .... + 594(1 + 52)]
= (1 + 52) (5 + ... + 593) + (1 + 52)(52 + ... + 594)
= (1 + 52)(5 + 52 + ... + 593 + 594)
= 26(5 + 52 + ... + 593 + 594)\(⋮\)26
d) B = 5 + 52 + 53 + 54 + 55 + 56 + .. 593 + 594 + 595 + 596
= (5 + 54) + (52 + 55) + (53 + 56) + ....+ (593 + 596)
= 5(1 + 53) + 52(1 + 53) + 53(1 + 53) + ... + 593(1 + 53)
= (1 + 53)(5 + 52 + 53 + .... + 593)
= 126(5 + 52 + 53 + .... + 593) \(⋮\)126
17 tháng 8 2020
a, B=5(1+5)+53(1+5)+...+595(1+5)
B=6(5+53+...+595)
=> B chia hết cho 6
b, B=5(1+5+52)+54(1+5+52)+...+594(1+5+52)
B=31(5+54+...+594)
=> B chia hết cho 31
c, B=(5+53)+(52+54)+...+(594+596)
B=5(1+52)+52(1+52)+...+594(1+52)
B=26(5+52+...+594)
=> B chia hết cho 26
d, B=(5+54)+(52+55)+...+(593+596)
B=5(1+53)+52(1+53)+...+593(1+53)
B=126(5+52+...+593)
=> B chia hết cho 126
Tích hộ mik nha <3
29 tháng 12 2021
Bài 4:
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
MU
3
31 tháng 8 2016
\(2x.\left(x-\frac{1}{7}\right)=0\)
=> \(\orbr{\begin{cases}2x=0\\x-\frac{1}{7}=0\end{cases}}\)=> \(\orbr{\begin{cases}x=0\\x=\frac{1}{7}\end{cases}}\)
7 tháng 6 2021
`k)(-12)/19=(-19+7)/19=-1+7/19`
`(-14)/17=(-17+3)/17=-1+3/17`
`3/17-7/19=-62/323<0`
`=>3/17<7/19`
`=>-1+3/17<-1+7/19`
`=>(-14)/17<(-12)/19`
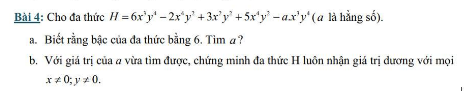
camon anh nhó'