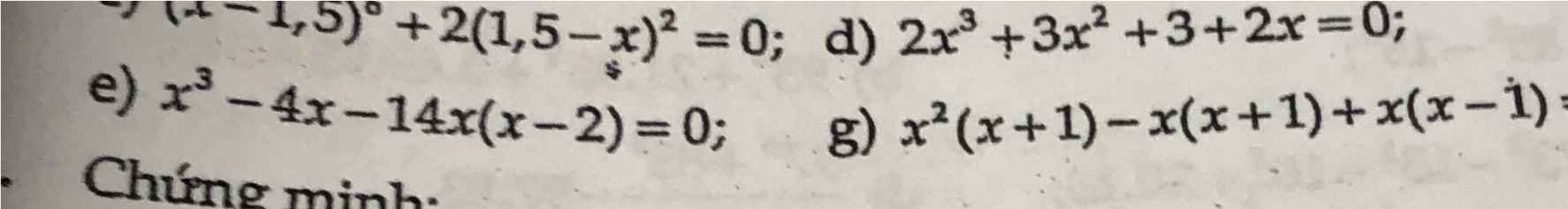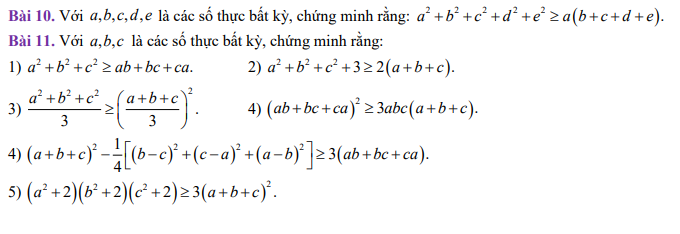K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 8 2021
e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
5 tháng 8 2021
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 7 2021
\(B=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(B_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(C=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
\(C_{min}=2\) khi \(\left(x;y\right)=\left(1;2\right)\)
1 tháng 7 2021
b) Ta có: \(B=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\forall x\)
Dấu '=' xảy ra khi x(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy: \(B_{min}=-36\) khi \(x\in\left\{0;-5\right\}\)
c) Ta có: \(C=x^2-2x+y^2-4y+7\)
\(=x^2-2x+1+y^2-4y+4+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: \(C_{min}=2\) khi (x,y)=(1;2)
MP
1
5 tháng 10 2021
Bài 2:
a: Ta có: \(M=2x\left(2x^3-3x\right)-x^2\left(3x^2-2\right)-x^2\left(x^2-4\right)\)
\(=4x^4-6x^2-3x^4+2x^2-x^4+4x^2\)
=0
b: Ta có: \(N=x\left(y^2-x\right)-y\left(xy-x^2\right)-x\left(xy-x-1\right)\)
\(=xy^2-x^2-xy^2+x^2y-x^2y+x^2+x\)
\(=x\)
NV
4
24 tháng 12 2021
7 + 4 = 11 chứ nhiu. cái câu này đến lớp 1 cũng biết hỏi. hỏi linh tinh
TA
3
23 tháng 9 2021
\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
23 tháng 9 2021
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)
CC
3
15 tháng 1 2019
Lấy K là trung điểm CD thì HK là đường trung bình \(\Delta\)BCD => HK // BD và HK=BD/2
Từ HK=BD/2 và AH=BD/2 => \(\Delta\)AHK cân tại H => ^HAK = ^HKA. Mà ^HKA = ^ADB (Do HK //BD)
Nên ^HAK = ^ADB = ^ABC/2 + ^ACB hay ^BAC/2 = ^ABC/2 + ^ACB
<=> ^BAC = ^ABC + 2^ACB. Từ đó ta có hệ: \(\hept{\begin{cases}\widehat{BAC}=\widehat{ABC}+2\widehat{ACB}\\\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\end{cases}}\)
Đến đây thì dễ rồi nhé !