K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
22 tháng 12 2021
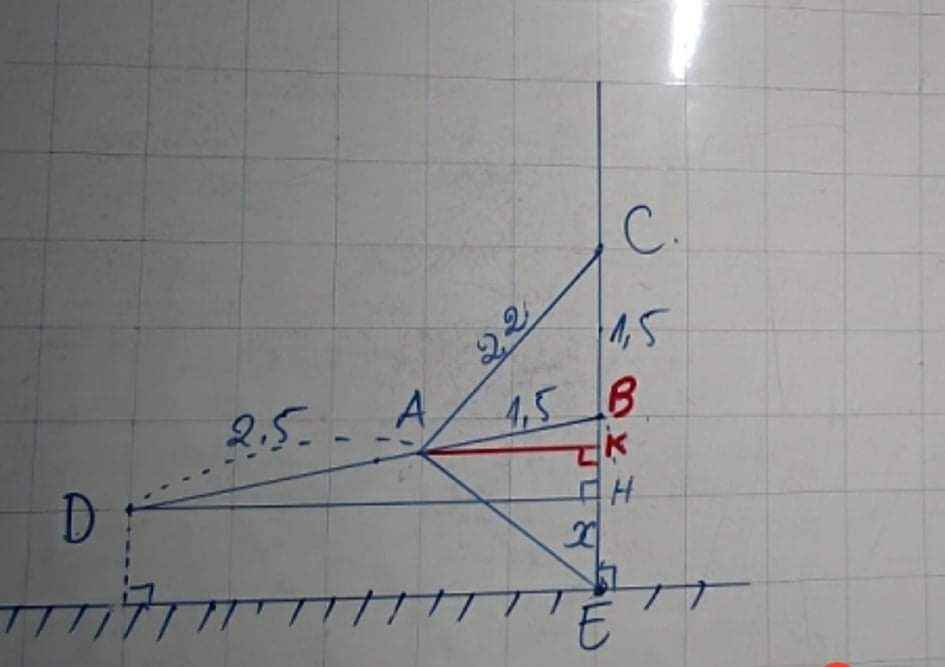
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)
22 tháng 3 2022
Gọi thời gian đội công nhân thứ nhất làm riêng xong công việc trên là x (ngày, x > 6)
Gọi thời gian đội công nhân thứ hai làm riêng xong công việc là y (ngày, y > 6)
Hệ phương trình của bạn đây:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{3}{x}+\dfrac{2}{y}=\dfrac{2}{5}\end{matrix}\right.\)
à mà mình không phải qtv
R
0
RK
23 tháng 6 2021
Mỗi một tháng người đó nhận được số tiền lãi là: \(100\cdot1,1\%=1,1\left(tr\right)\)
a) Đổi: 4 năm = 48 tháng
=> Sau 4 năm người đó thu về số tiền là:
$sau 4 năm = $gốc + $lãi
= 100 + 48 . 1,1 = 152,8 (triệu)
b) Mỗi tháng người đó mất: 4 - 1,1 = 2,9 (triệu)
=> Số tháng mà người đó sẽ tiêu hết số tiền là: 100 : 2,9 \(\cong34,5\left(th\right)\)
TH
0
9 tháng 12 2023
Câu 2:
1: \(y=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)x+4=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)\cdot x=\sqrt{3}+5-4=\sqrt{3}+1\)
=>\(x=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=\dfrac{\left(\sqrt{3}+1\right)^2}{3-1}=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\)
2: \(x^2-2\left(1-m\right)x-2m-5=0\)
=>\(x^2+\left(2m-2\right)x-2m-5=0\)
a: \(\Delta=\left(2m-2\right)^2-4\left(-2m-5\right)\)
\(=4m^2-8m+4+8m+20\)
\(=4m^2+24>=24>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Câu 1:
2: Thay x=2 và y=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a-\left(-1\right)=5\\b\cdot2+a\cdot\left(-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=5+\left(-1\right)=4\\2b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\2b=a+4=6\end{matrix}\right.\)
=>a=2 và b=3
2: Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\left(b\ne0\right)\)
Khi tăng mẫu số thêm 4 đơn vị thì phân số đó bằng 1/3 nên ta có:
\(\dfrac{a}{b+4}=\dfrac{1}{3}\)
=>3a=b+4
=>3a-b=4(1)
Khi giảm mẫu số đi 2 đơn vị thì phân số bằng với 2/3 nên ta có:
\(\dfrac{a}{b-2}=\dfrac{2}{3}\)
=>3a=2(b-2)
=>3a=2b-4
=>3a-2b=-4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=4\\3a-2b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\3a-b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=8\\3a=b+4=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=8\end{matrix}\right.\)(nhận)
Vậy: Phân số cần tìm là \(\dfrac{4}{8}\)
TH
1
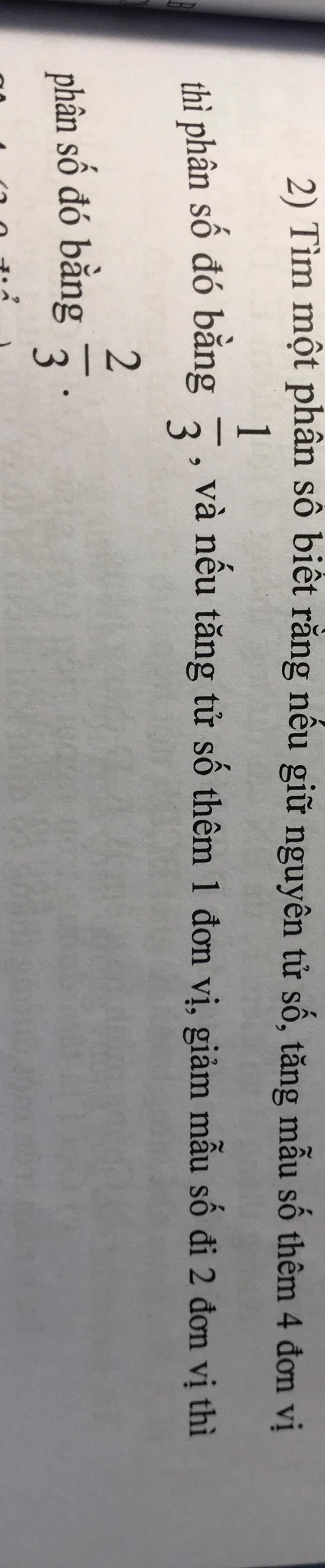
Xét tam giác ABC vuông tại A có:
AC = AB.tan\(\widehat{ABC}\) = 4,5467. tan59o12'37'' \(\approx\) 7,6303 (cm)
BC = \(\dfrac{AB}{cos\widehat{ABC}}=\dfrac{4,5467}{cos59^o12'37"}\)\(\approx\) 8,8822 (cm)
Do AM là trung tuyến tam giác ABC
=> AM = MC = MB = \(\dfrac{1}{2}\)AB \(\approx\) \(\dfrac{1}{2}\).8,8822 = 4,4411 (cm)
Kẻ NK ⊥ AC => NK // AB (cùng vuông góc AC)
AN là phân giác trong tam giác ABC =>\(\widehat{NAB}=\widehat{NAC}=45^o\); \(\dfrac{NC}{NB}=\dfrac{AC}{AB}=\dfrac{7,6303}{4,5467}\) => \(\dfrac{NC}{BC}=\dfrac{7,6303}{12,177}\) (*)
Do NK // AB (cmt) => \(\dfrac{NK}{AB}=\) \(\dfrac{NC}{BC}=\dfrac{7,6303}{12,177}\)
=> NK = \(\dfrac{7,6303}{12,177}.AB=\dfrac{7,6303}{12,177}.4,5467\approx2,849\) (cm)
Xét tam giác ANK vuông tại K có: AN = \(\dfrac{NK}{sin\widehat{NAK}}=\dfrac{2,849}{sin45^o}\approx2,015\left(cm\right)\)
Kẻ AH ⊥ BC. Xét tam giác ABC vuông tại A có: AH.BC = AB.AC
=> AH = \(\dfrac{AB.AC}{BC}=\dfrac{4,5467.7,6303}{8,8822}\approx3,9509\left(cm\right)\)
Từ (*) => NC = \(\dfrac{7,6303}{12,177}.BC=\dfrac{7,6303}{12,177}.8,8822\approx5,5657\) (cm)
=> MN = NC - MC = 5,5657 - 4,4411 = 1,1246 (cm)
=> SAMN = \(\dfrac{1}{2}\).AH.MN = \(\dfrac{1}{2}\).3,9509.1,1246 \(\approx\) 2,2216 (cm2)