
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Ta có: ΔOEF cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)EF
Xét tứ giác OIMP có \(\widehat{OIP}=\widehat{OMP}=90^0\)
nên OIMP là tứ giác nội tiếp
2: Xét ΔOMP vuông tại M có MH là đường cao
nên \(OH\cdot OP=OM^2=OF^2\)
=>\(\dfrac{OH}{OF}=\dfrac{OF}{OP}\)
Xét ΔOHF và ΔOFP có
\(\dfrac{OH}{OF}=\dfrac{OF}{OP}\)
\(\widehat{HOF}\) chung
Do đó: ΔOHF~ΔOFP

Câu 2:
1: \(y=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)x+4=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)\cdot x=\sqrt{3}+5-4=\sqrt{3}+1\)
=>\(x=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=\dfrac{\left(\sqrt{3}+1\right)^2}{3-1}=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\)
2: \(x^2-2\left(1-m\right)x-2m-5=0\)
=>\(x^2+\left(2m-2\right)x-2m-5=0\)
a: \(\Delta=\left(2m-2\right)^2-4\left(-2m-5\right)\)
\(=4m^2-8m+4+8m+20\)
\(=4m^2+24>=24>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Câu 1:
2: Thay x=2 và y=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a-\left(-1\right)=5\\b\cdot2+a\cdot\left(-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=5+\left(-1\right)=4\\2b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\2b=a+4=6\end{matrix}\right.\)
=>a=2 và b=3
2: Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\left(b\ne0\right)\)
Khi tăng mẫu số thêm 4 đơn vị thì phân số đó bằng 1/3 nên ta có:
\(\dfrac{a}{b+4}=\dfrac{1}{3}\)
=>3a=b+4
=>3a-b=4(1)
Khi giảm mẫu số đi 2 đơn vị thì phân số bằng với 2/3 nên ta có:
\(\dfrac{a}{b-2}=\dfrac{2}{3}\)
=>3a=2(b-2)
=>3a=2b-4
=>3a-2b=-4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=4\\3a-2b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\3a-b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=8\\3a=b+4=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=8\end{matrix}\right.\)(nhận)
Vậy: Phân số cần tìm là \(\dfrac{4}{8}\)


b: kẻ đường kính AD
góc ACD=90 độ=góc ABD
=>AC vuông góc CD và AB vuông góc BD
=>BH//CD và CH//BD
=>BDCH là hbh
=>H,N,D thẳng hàng và N là trung điểm của HD
=>NT là đường trung bình của ΔAHD
=>NT//AD và NT=1/2AD=OA
=>NT//OA
=>ATNO là hbh
EN=1/2BC
=>EN=BN
=>ΔNEB cân tại N
=>góc NBE=góc NEB
EJ=1/2AH=JH
=>ΔJEH cân tại J
=>góc JEH=góc JHE
góc NBE+Góc ACB=90 độ
góc HAC+góc ACB=90 độ
=>góc NBE=góc HAC
mà góc JHE+góc HAC=90 độ
nên góc JHE+góc NBE=90 độ
=>góc JEN=90 độ

\(C=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)-\sqrt{x}\left(\sqrt{x}+2\right)+6\sqrt{x}}{x-4}.\left(x-4\right)=2\sqrt{x}\)



10:
\(a+b=50^0+40^0=90^0\)
=>\(sina=cosb;sinb=cosa;tana=cotb;cota=tanb\)
=>sina=cosb
=>Chọn C
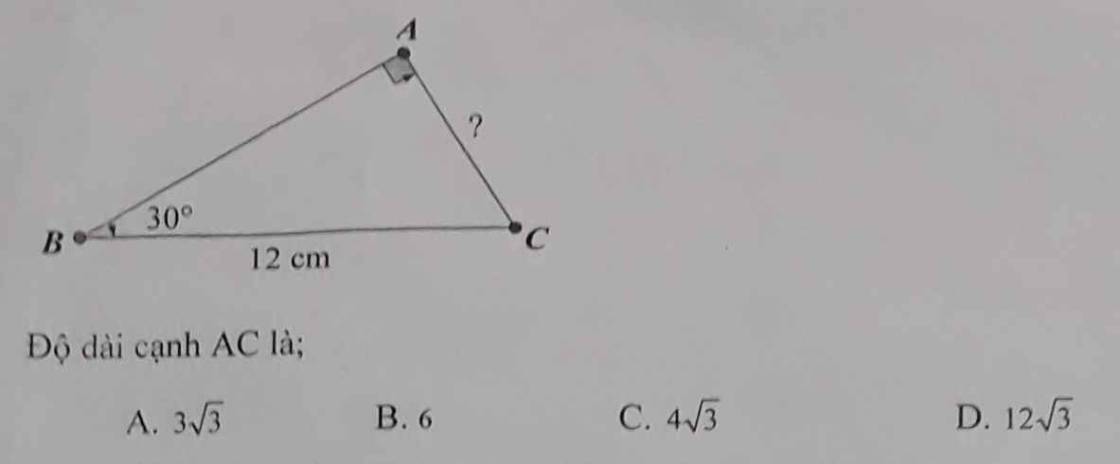
11:
Xét ΔABC vuông tại A có \(AC=BC\cdot sinB\)
=>\(AC=12\cdot sin30=6\)
=>Chọn B

Lời giải:
Vì $(d)$ đi qua điểm $M(2,3)$ nên:
$y_M=ax_M+b\Leftrightarrow 3=2a+b(1)$
Vì $(d)$ cắt trục tung tại điểm có tung độ 2, tức là $(d)$ cắt trục tung tại điểm $(0,2)$
$\Rightarrow 2=a.0+b(2)$
Từ $(1); (2)\Rightarrow b=2; a=\frac{1}{2}$

2: Để (d)//y=(m2+1)x-4 thì \(\left\{{}\begin{matrix}m^2=1\\m-5\ne-4\end{matrix}\right.\Leftrightarrow m=1\)



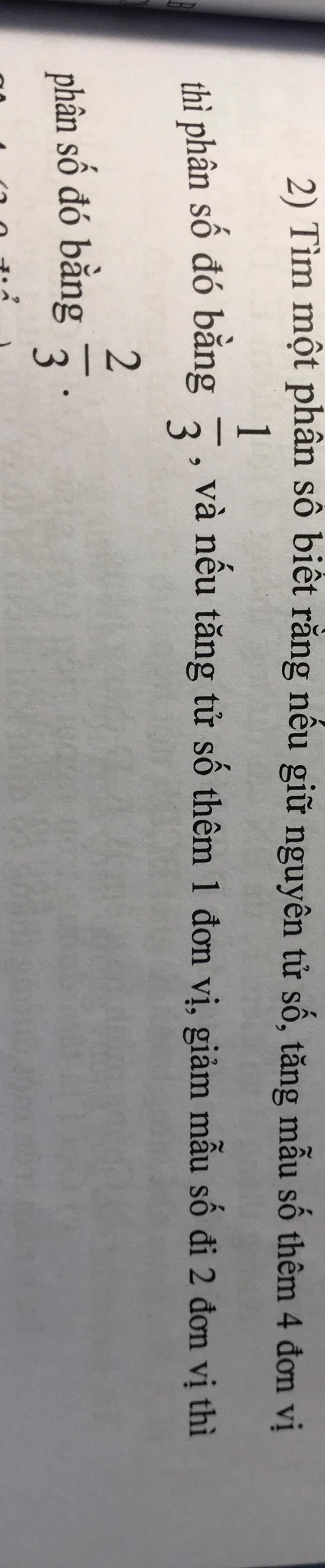


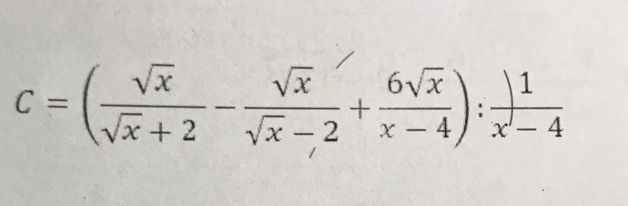



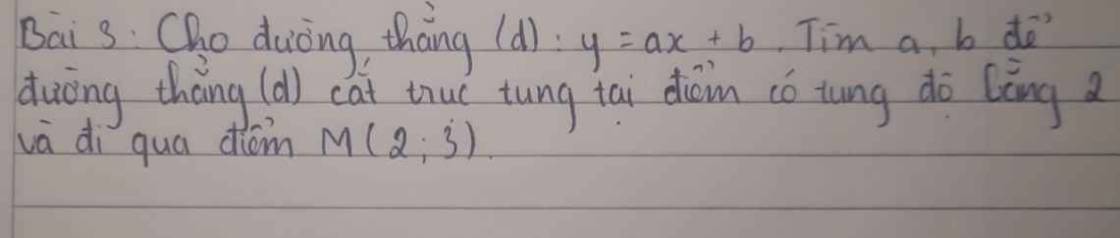

a: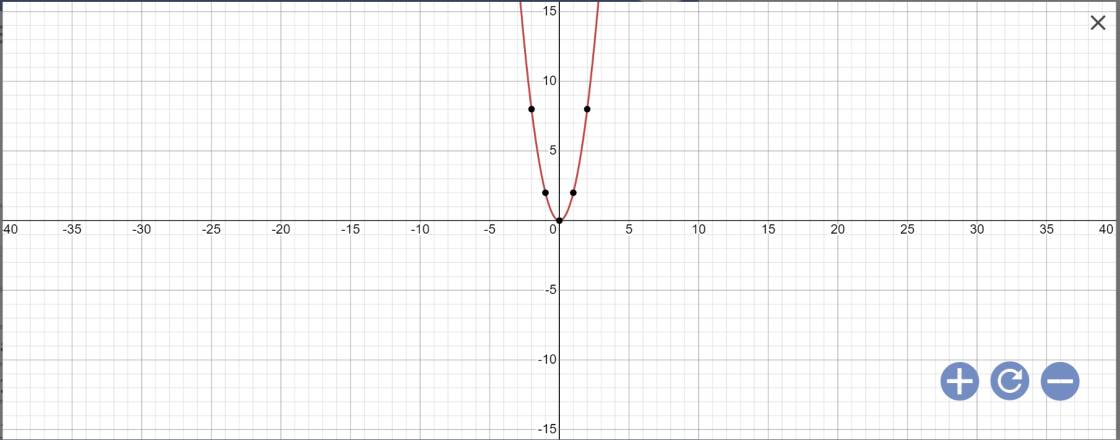
b: Phương trình hoành độ giao điểm là:
\(2x^2=3x-1\)
=>\(2x^2-3x+1=0\)
=>(x-1)(2x-1)=0
=>\(\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)
Khi x=1 thì \(y=2\cdot x^2=2\cdot1^2=2\)
Khi x=1/2 thì \(y=2\cdot\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
Vậy: (P) giao (Δ) tại A(1;2); B(1/2;1/2)
c: Phương trình hoành độ giao điểm là:
\(2x^2=-2\left(m-2\right)x-2m+6\)
=>\(2x^2+2\left(m-2\right)x+2m-6=0\)
=>\(x^2+\left(m-2\right)x+m-3=0\)
\(\text{Δ}=\left(m-2\right)^2-4\left(m-3\right)\)
\(=m^2-4m+4-4m+12=m^2-8m+16=\left(m-4\right)^2\)
Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0
=>\(\left(m-4\right)^2>0\)
=>\(m-4\ne0\)
=>\(m\ne4\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-m+2\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)
\(2x_1x_2-\left(x_1-x_2\right)^2=-1\)
=>\(2x_1x_2-\left[\left(x_1+x_2\right)^2-4x_1x_2\right]=-1\)
=>\(-\left(x_1+x_2\right)^2+6x_1x_2=-1\)
=>\(-\left(-m+2\right)^2+6\left(m-3\right)=-1\)
=>\(-m^2+4m-4+6m-18+1=0\)
=>\(-m^2+10m-21=0\)
=>\(\left(m-3\right)\left(m-7\right)=0\)
=>\(\left[{}\begin{matrix}m=3\left(nhận\right)\\m=7\left(nhận\right)\end{matrix}\right.\)