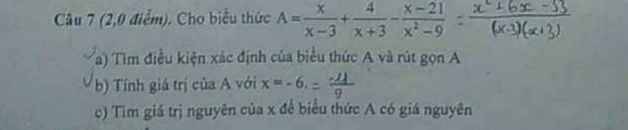K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 8 2021
Bài 7:
b: Ta có: \(B=\left(x-9\right)\left(2x+3\right)-2\left(x+7\right)\left(x-5\right)\)
\(=2x^2+3x-18x-27-2\left(x^2+2x-35\right)\)
\(=2x^2-15x-27-2x^2-4x+70\)
\(=-19x+57\)
\(=-19\cdot\dfrac{1}{2}+57=\dfrac{95}{2}\)
c: Ta có: \(C=\left(-5x+4\right)\left(3x-2\right)+\left(-2x+3\right)\left(x-2\right)\)
\(=-15x^2+10x+12x-8-2x^2+4x+3x-6\)
\(=-17x^2+29x-14\)
\(=-17\cdot4-29\cdot2-14=-140\)
LP
11 tháng 8 2021
7c)Ta có :C\(=\left(-5x+4\right)\left(3x-2\right)+\left(-2x+3\right)\left(x-2\right)\)
Tại x=-2 thì giá trị của biểu thức C là:
C=\(\left[-5.\left(-2\right)+4\right]\left[3.\left(-2\right)-2\right]+\left[-2\left(-2\right)+3\right]\left[-2-2\right]\)
C=\(14.\left(-8\right)+4.\left(-4\right)\)
C=\(-112-16=-140\)
Vậy tại x=-2 thì giá trị của biểu thức C =-140
MD
1
YN
28 tháng 4 2022
\(x^7+x^2+1\)
\(=\left(x^7-x\right)+\left(x^2+x+1\right)\)
\(=x.\left(x^6-1\right)+\left(x^2+x+1\right)\)
\(=x.\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right).\left[\left(x^2-x\right)\left(x^3+1\right)+1\right]\)
\(=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)
28 tháng 9 2016
Câu 1:\(x^2.y+x.y^2-x-y=x.\left(x.y-1\right)+y.\left(x.y-1\right)=\left(x+y\right).\left(x.y-1\right)\)
Câu 3:\(a.x^2+a.y-b.x^2-b.y=x^2.\left(a-b\right)+y.\left(a-b\right)=\left(x^2+y\right).\left(a-b\right)\)
PQ
2
14 tháng 4 2021
a) Xét ΔMNI vuông tại M và ΔHPI vuông tại P có
\(\widehat{MIN}=\widehat{HIP}\)(hai góc đối đỉnh)
Do đó: ΔMNI\(\sim\)ΔHPI(g-g)
14 tháng 4 2021
b) Ta có: ΔMNI\(\sim\)ΔHPI(cmt)
nên \(\widehat{MNI}=\widehat{HPI}\)(hai góc tương ứng)
hay \(\widehat{MNI}=\widehat{MPK}\)
Xét ΔMNI vuông tại M và ΔMPK vuông tại M có
\(\widehat{MNI}=\widehat{MPK}\)(cmt)
Do đó: ΔMNI\(\sim\)ΔMPK(g-g)
Suy ra: \(\dfrac{MN}{MP}=\dfrac{MI}{MK}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)
Xét ΔMNP vuông tại M và ΔMIK vuông tại M có
\(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)(cmt)
Do đó: ΔMNP\(\sim\)ΔMIK(c-g-c)
VT
1
22 tháng 10 2021
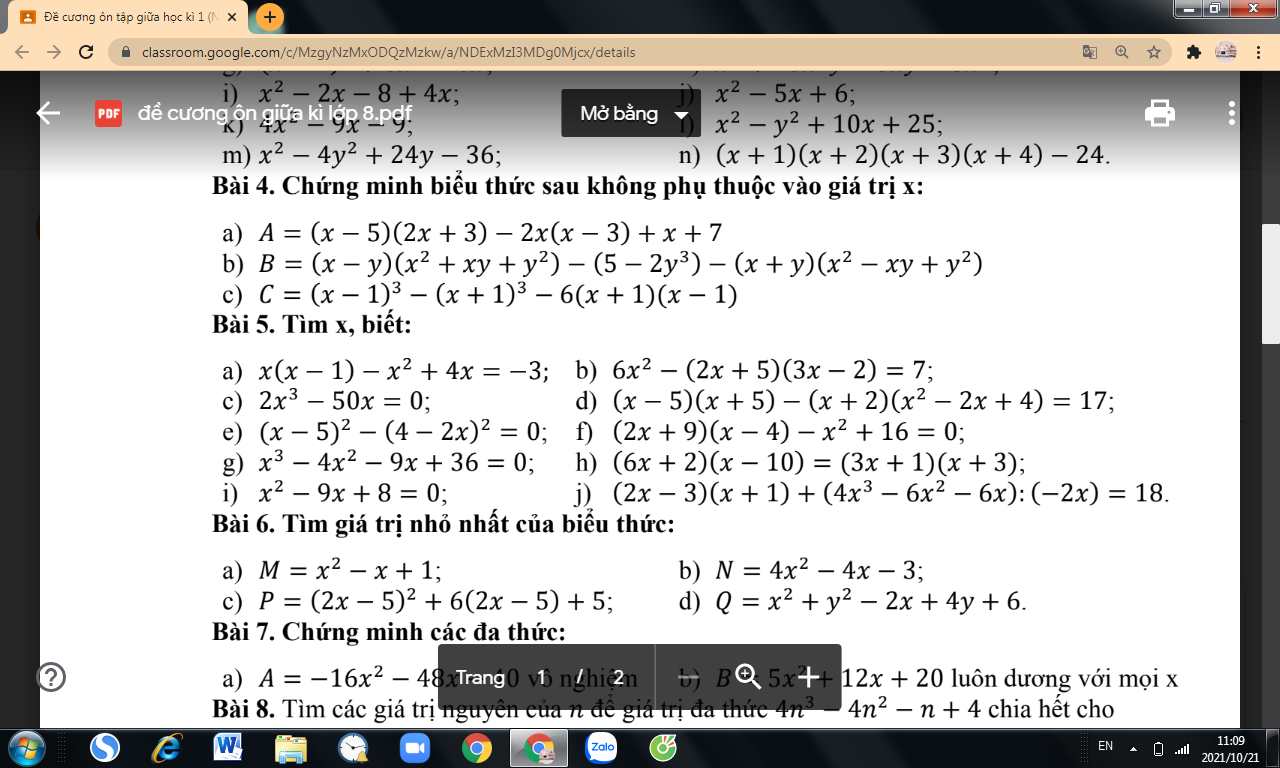
c: \(2x^3-50x=0\)
\(\Leftrightarrow2x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
PT
2
25 tháng 2 2022
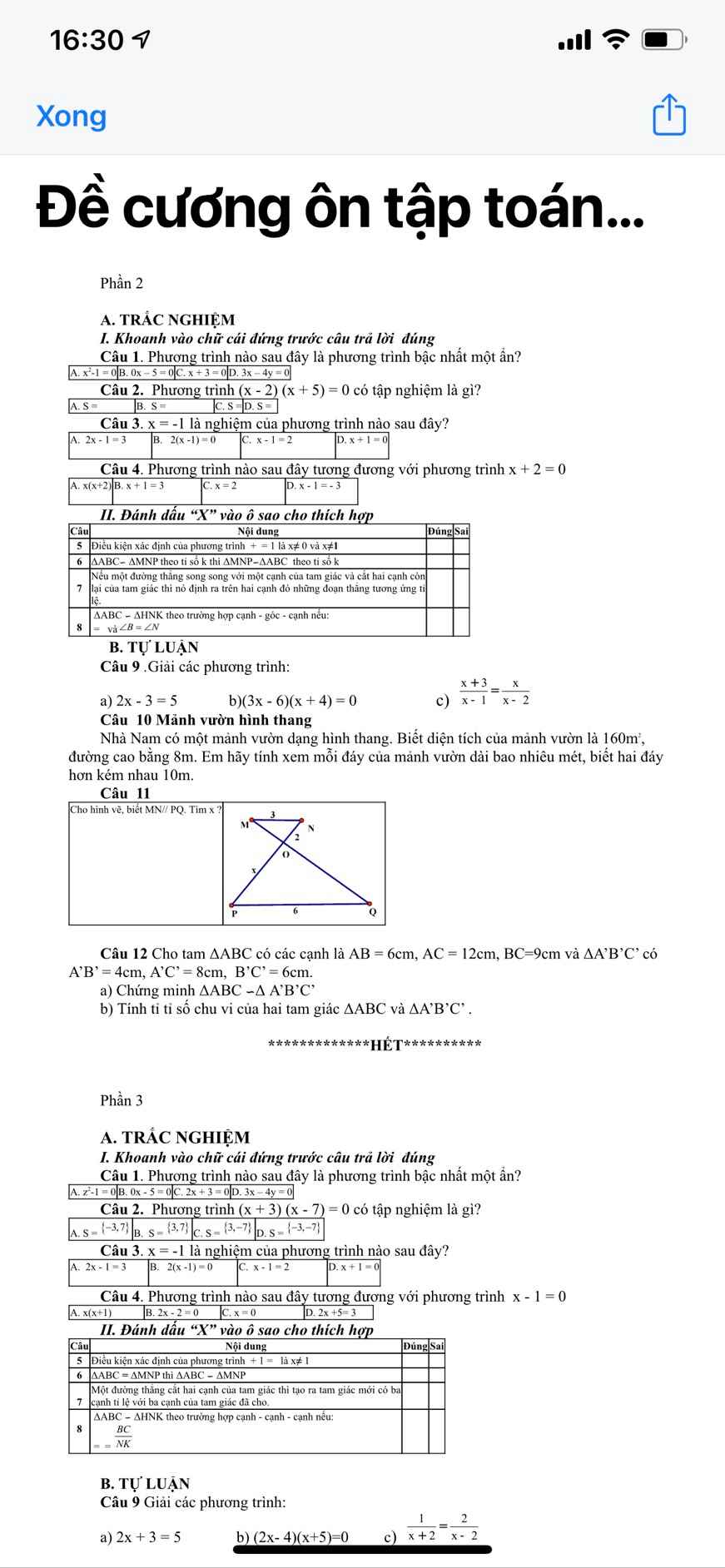
Câu 9:
a: 2x+3=5
nên 2x=2
hay x=1
b: (2x-4)(x+5)=0
=>(x-2)(x+5)=0
=>x-2=0 hoặc x+5=0
=>x=2 hoặc x=-5
c: 1/x+2=2/x-2
=>2x+4=x-2
=>x=-6
20 tháng 5 2022
a: \(P=\left(\dfrac{x}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{x\left(x+5\right)}\right)\cdot\dfrac{x\left(x+5\right)}{2x-5}+\dfrac{x^2}{5-x}\)
\(=\dfrac{x^2-x^2+10x-25}{\left(x-5\right)\left(x+5\right)}\cdot\dfrac{x\left(x+5\right)}{2x-5}-\dfrac{x^2}{x-5}\)
\(=\dfrac{5\left(2x-5\right)\cdot x}{\left(x-5\right)\left(2x-5\right)}-\dfrac{x^2}{x-5}=\dfrac{5x-x^2}{x-5}=-x\)
b: Để P là số nguyên thì x là số nguyên