
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Mình trình bày cho dễ hiểu nha
\(sina-\sqrt{3}cosa\)
\(=2\cdot\left(\frac{1}{2}sina-\frac{\sqrt{3}}{2}cosa\right)\)
\(=2\cdot\left(sinacos\frac{pi}{6}-cosasin\frac{pi}{6}\right)\)
\(=2\cdot sin\left(a-\frac{pi}{6}\right)\)
Ta có\(-1\le sin\left(a-\frac{pi}{6}\right)\le1\)
\(-2\le sin\left(a-\frac{pi}{6}\right)\le2\)
Vậy Min=-2
Max=2


Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
DO đó; OM là tia phân giác của góc AOB
Xét ΔOAM vuông tại A có
\(\tan\widehat{AOM}=\dfrac{AM}{AO}=\sqrt{3}\)
nên \(\widehat{AOM}=60^0\)
=>\(\widehat{AOB}=120^0\)

câu 1:
a2+b2+c2+42 = 2a+8b+10c
<=> a2-2a+1+b2 -8b+16+c2-10c+25=0
<=> (a-1)2+(b-4)2+(c-5)2=0
<=>a=1 và b=4 và c=5
=> a+b+c = 10
ta có 2(a2+b2)=5ab
<=> 2a2+2b2-5ab=0
<=> 2a2-4ab-ab+2b2=0
<=> 2a(a-2b)-b(a-2b)=0
<=> (a-2b)(2a-b)=0
<=> a=2b(thỏa mãn)
hoặc b=2a( loại vì a>b)
với a=2b =>P=5b/5b=1

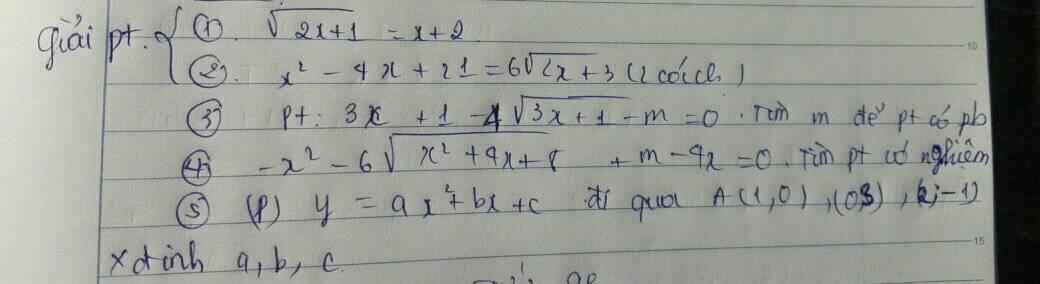 giúp em câu 3,4 với ạ
giúp em câu 3,4 với ạ



 mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha
mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha














1.
\(\sqrt{2x+1}=x+2\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+1\ge0\\2x+1=\left(x+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\2x+1=x^2+4x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x^2+2x+3=0\left(vn\right)\end{matrix}\right.\)
Phương trình đã cho vô nghiệm
2.
ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
C1:
\(x^2-4x+21=6\sqrt{2x+3}\)
\(\Leftrightarrow\left(x^2-6x+9\right)+\left(2x+3-6\sqrt{2x+3}+9\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(\sqrt{2x+3}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\\sqrt{2x+3}-3=0\end{matrix}\right.\)
\(\Leftrightarrow x=3\)
C2:
\(x^2-4x+21=2.3.\sqrt{2x+3}\)
\(\Rightarrow x^2-4x+21\le3^2+2x+3\)
\(\Rightarrow x^2-6x+9\le0\)
\(\Rightarrow\left(x-3\right)^2\le0\)
\(\Rightarrow x-3=0\)
\(\Rightarrow x=3\)