
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
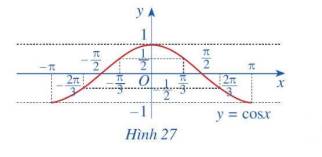
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
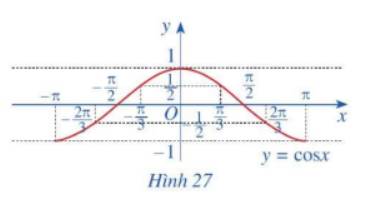
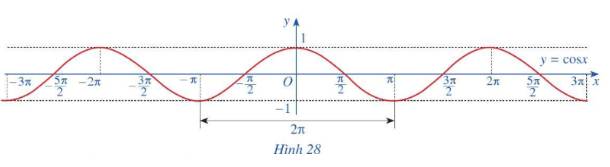
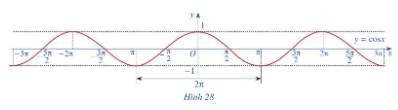
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

Tham khảo:
Mẫu a, b là mẫu số liệu ghép nhóm.
a)

- Có 5 sinh viên chi dưới 50 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 12 sinh viên chi từ 50 đến dưới 100 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 23 sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 17 sinh viên chi từ 150 đến dưới 200 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 3 sinh viên chi từ 200 đến dưới 250 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
Như vậy, đa số sinh viên chi từ 100 đến dưới 150 nghìn đồng mỗi tháng cho cước điện thoại và có ít sinh viên chi trên 200 nghìn đồng cho cước điện thoại mỗi tháng.
b)

- Có 7 ngày có nhiệt độ từ đến dưới.
- Có 15 ngày có nhiệt độ từ đến dưới.
- Có 12 ngày có nhiệt độ từ đến dưới.
- Có 6 ngày có nhiệt độ từ đến dưới.



bài này dễ thôi bạn
thay x= x+ k6pi vào hàm số y=f(x)= sin\(\frac{x}{3}\) ta dc
sin\(\frac{x+k6pi}{3}\) =sin\(\frac{x}{3}+k2pi\) ( vì k2pi "số chẵn lần của π" nên có thể bỏ được)
suy ra sin\(\frac{x}{3}\) =sin\(\frac{x}{3}\) =f(x) ( dpcm)

Gọi \(\overline{abcde}\)là số cần tìm.
Vì \(\overline{abcde}\)là số chẵn nên \(e\in\left\{0;2;4;6;8\right\}\)
*Trường hợp 1: e=0
Có 2 cách chọn a(\(a\ne e\)và \(a\le2\))
Có 3 cách chọn b(\(b\ne a\ne e\)và b<5)
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân ta được:2.3.4.3.1=72 số
*Trường hợp 2: e=2
Có 1 cách chọn a
Có 3 cách chọn b
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân có 1.3.4.3.1=24 số
*Trường hợp 3:e=4
Có 2 cách chọn a
Có 3 cách chọn b
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân có: 2.3.4.3.1=72 số
*Trường hợp 4:\(e\in\left\{6;8\right\}\)
Có 2 cách chon a
Có 4 cách chọn b
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân có:2.4.4.3.2=192 số
Vậy số các số chẵn có 5 chữ số khác nhau và nhỏ hơn 25000 là:72+24+72+192=360 số





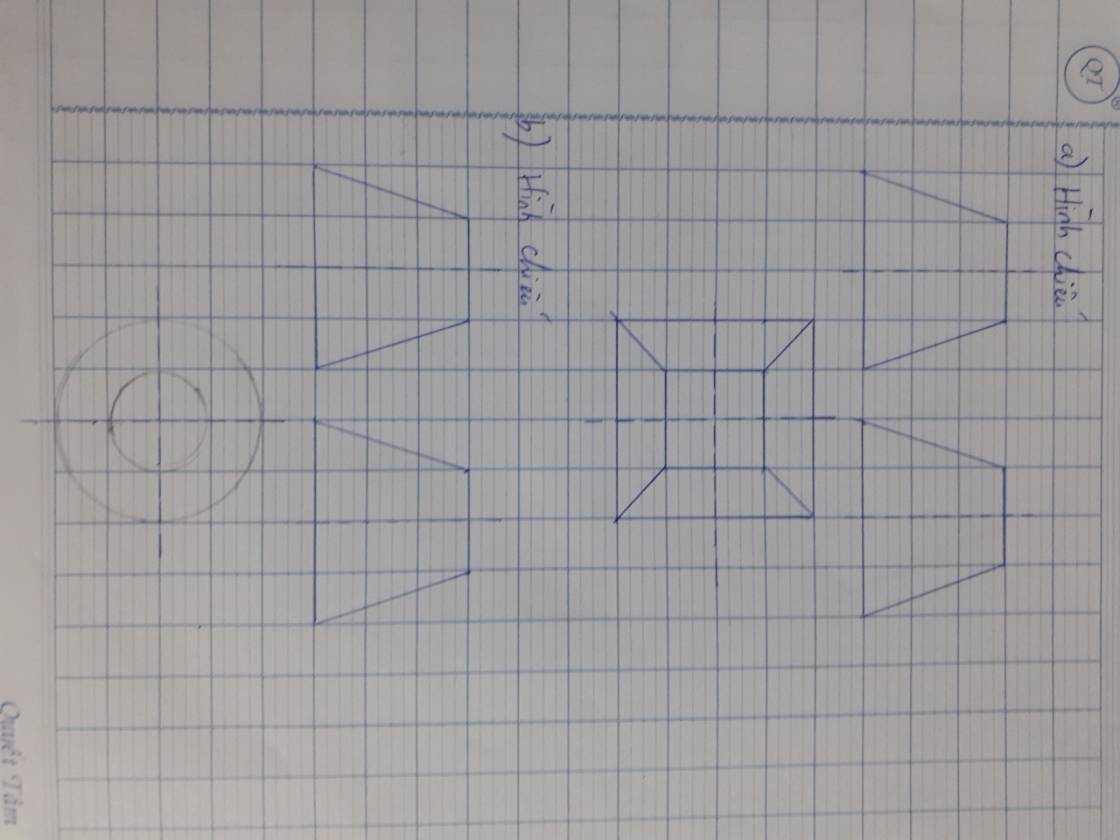
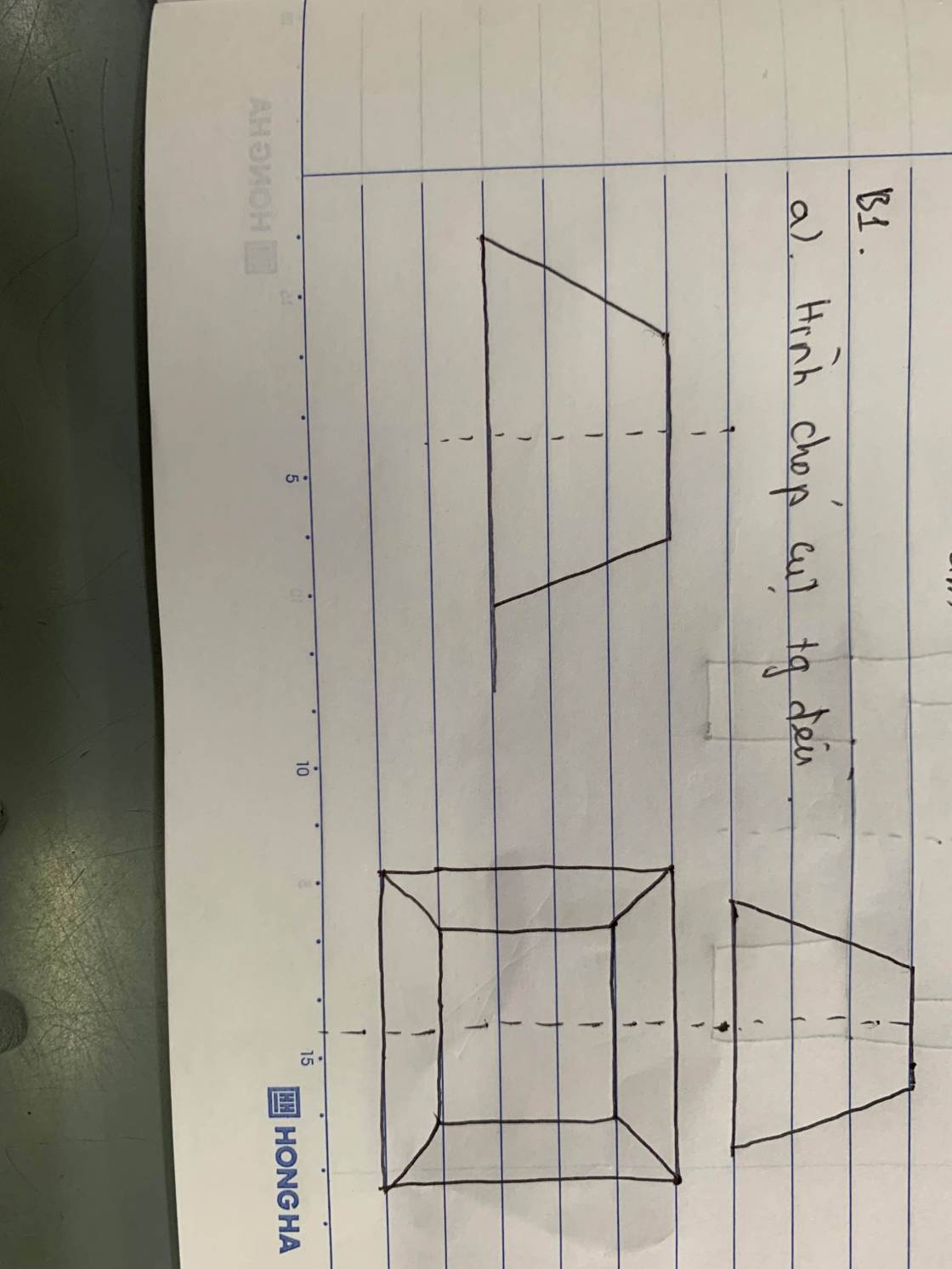
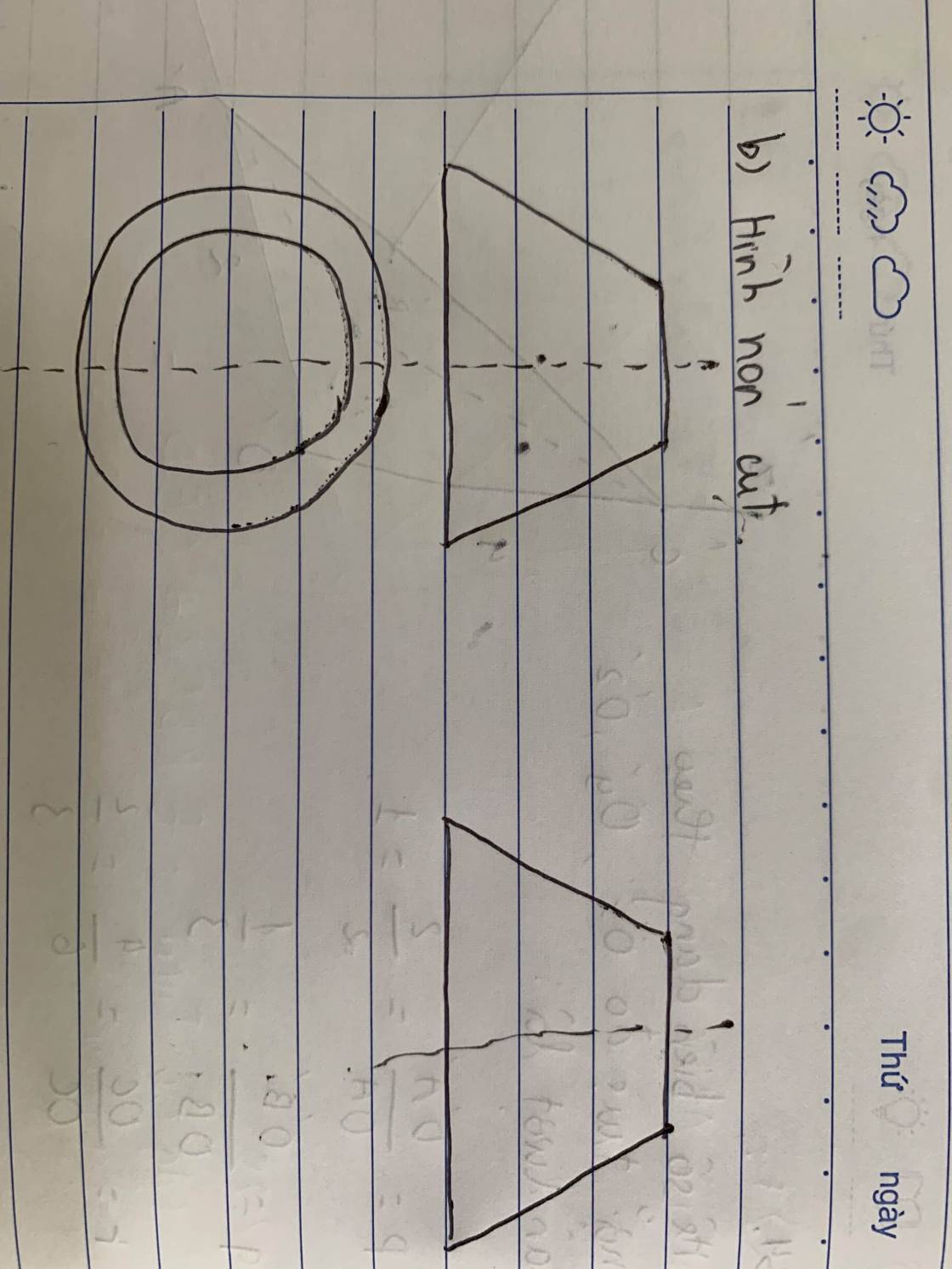


 giúp t với ạ
giúp t với ạ
 giúp mình với ạ
giúp mình với ạ em đang bí quá, giúp em với ạ, đề thi thử toán 11
em đang bí quá, giúp em với ạ, đề thi thử toán 11

a: \(N\in SB\subset\left(SBC\right)\)
\(N\in\left(NAD\right)\)
Do đó: \(N\in\left(SBC\right)\cap\left(NAD\right)\)
Xét (SBC) và (NAD) có
\(N\in\left(SBC\right)\cap\left(NAD\right)\)
BC//AD
Do đó: (SBC) giao (NAD)=xy, xy đi qua N và xy//BC//AD
b: Trong mp(ABCD), Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\left(1\right)\)
\(S\in SA\subset\left(SAC\right)\)
\(S\in SB\subset\left(SBD\right)\)
Do đó: \(S\in\left(SAC\right)\cap\left(SBD\right)\left(2\right)\)
Từ (1) và (2) suy ra (SAC) giao (SBD)=SO
c: Chọn mp(SBC) có chứa NK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SCA\right)\)
Do đó: \(\left(SBC\right)\cap\left(SCA\right)=SC\)
Gọi E là giao điểm của NK với SC
=>E là giao điểm của NK với mp(SAC)
d: Chọn mp(SBD) có chứa DN
Ta có: (SBD) giao (SAC)=SO(cmt)
nên ta sẽ gọi F là giao điểm của SO với DN
=>F là giao điểm của ND với mp(SAC)
e: Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình của ΔSAB
=>MN//AB và \(MN=\dfrac{AB}{2}\)
MN//AB
AB//CD
Do đó: MN//CD
Xét tứ giác MNCD có MN//CD
nên MNCD là hình thang