K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
18 tháng 3 2022
\(L=\lim\limits_{x\rightarrow+\infty}\left(2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\right)\)
Đặt \(f\left(x\right)=2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\)
Ta có:
\(2.f\left(x\right)=4x^2-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(4x^2-1\right)-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)+\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
Đặt \(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(=\dfrac{\left(2x-1\right)\left(8x^3+12x^2+6x+1-8x^3-12x^2+3x\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(=\dfrac{\left(2x-1\right)\left(9x+1\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}A\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2-\dfrac{1}{x}\right)\left(9+\dfrac{1}{x}\right)}{\left(2+\dfrac{1}{x}\right)^2+\sqrt[3]{\left(8+\dfrac{12}{x}-\dfrac{3}{x^2}\right)^2}+\left(2+\dfrac{1}{x}\right)\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}\)
\(=\dfrac{2.9}{2^2+4+2.2}\)
\(=\dfrac{3}{2}\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(=\dfrac{\left(4x^2-4x+1-4x^2+4x\right).\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(=\dfrac{\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}B\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}{2-\dfrac{1}{x}+\sqrt{4-\dfrac{4}{x}}}\)
\(=\dfrac{2}{2+2}\)
\(=\dfrac{1}{2}\)
\(\Rightarrow2L=\lim\limits_{x\rightarrow+\infty}\left[2f\left(x\right)\right]\)
\(=\lim\limits_{x\rightarrow+\infty}\left[1+A\left(x\right)+B\left(x\right)\right]\)
\(=1+\lim\limits_{x\rightarrow+\infty}A\left(x\right)+\lim\limits_{x\rightarrow+\infty}B\left(x\right)\)
\(=1+\dfrac{3}{2}+\dfrac{1}{2}\)
\(=3\)
\(\Rightarrow L=\dfrac{3}{2}\)
KN
1
HN
1
HP
19 tháng 12 2021
\(\left\{{}\begin{matrix}6u_2+u_5=1\\3u_3+2u_4=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6u_1.q+u_1.q^4=1\\3u_1.q^2+2u_1.q^3=-1\end{matrix}\right.\)
\(\Rightarrow u_1\left(6q+q^4+3q^2+2q^3\right)=0\)
\(\Leftrightarrow q^3+2q^2+3q+6=0\)
\(\Leftrightarrow\left(q+2\right)\left(q^2+3\right)=0\)
\(\Leftrightarrow q=-\text{}2\)
\(\Rightarrow u_1=\dfrac{1}{4}\)
\(\Rightarrow u_n=u_1.q^{n-1}=\dfrac{1}{4}.\left(-2\right)^{n-1}=\left(-2\right)^{n-3}\)
3 tháng 12 2023
a: \(G\in\left(SAD\right)\)
\(G\in GB\subset\left(GBC\right)\)
Do đó: \(G\in\left(SAD\right)\cap\left(GBC\right)\)
Xét (SAD) và (GBC) có
\(G\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó:(SAD) giao (SBC)=xy,xy đi qua G và xy//AD//BC
b: ABCD là hình bình hành tâm O
nên O là trung điểm chung của AC và BD
Xét ΔACB có
I,O lần lượt là trung điểm của CB,CA
=>IO là đường trung bình của ΔCAB
=>IO//AB
IO//AB
AB\(\subset\)(SAB)
IO không thuộc mp(SAB)
Do đó: IO//(SAB)
c: Xét ΔSAC có
H,O lần lượt là trung điểm của CS,CA
=>HO là đường trung bình của ΔSAC
=>HO//SA
HO//SA
SA\(\subset\)(SAB)
HO không nằm trong mp(SAB)
Do đó: HO//(SAB)
Ta có: IO//(SAB)
HO//(SAB)
IO,HO\(\subset\)(OHI)
Do đó: (OHI)//(SAB)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)
HP
1 tháng 8 2021
f, \(3sin^2x-cosx+2cos2x-3=0\)
\(\Leftrightarrow3-3cos^2x-cosx+2\left(2cos^2x-1\right)-3=0\)
\(\Leftrightarrow cos^2x-cosx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\cosx=2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pi+k2\pi\)
HP
1 tháng 8 2021
h, \(cos^2x+cos^22x+cos^23x+cos^24x=2\)
\(\Leftrightarrow2cos^2x+2cos^22x+2cos^23x+2cos^24x=4\)
\(\Leftrightarrow cos2x+cos4x+cos6x+cos8x=0\)
\(\Leftrightarrow2cos5x.cos3x+2cos5x.cosx=0\)
\(\Leftrightarrow cos5x\left(cos3x+cosx\right)=0\)
\(\Leftrightarrow2cos5x.cos2x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=0\\cos2x=0\\cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}+k\pi\\2x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{10}+\dfrac{k\pi}{5}\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
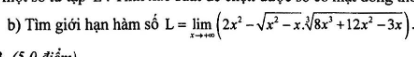
Đặt \(f\left(x\right)=x^2sinx+x.cosx+1\)
Hàm \(f\left(x\right)\) liên tục trên mọi khoảng thuộc R
Ta có: \(f\left(0\right)=1>0\)
\(f\left(\pi\right)=-\pi+1< 0\)
\(\Rightarrow f\left(0\right).f\left(\pi\right)< 0\Rightarrow\) phương trình \(f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\pi\right)\)
Hay pt đã cho luôn có nghiệm trên R
Em cảm ơn ạ