
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a,Áp dụng BĐT Cosi ta có:
\(a^2+\dfrac{1}{a^2}\ge2\sqrt{a^2.\dfrac{1}{a^2}}=2.1=2\)
dấu "=" xảy ra \(\Leftrightarrow a^2=\dfrac{1}{a^2} \Leftrightarrow a^4=1\Leftrightarrow a=\pm 1\)


a) Thay \(x=-3;y=2\) vào PT (d) ta được:
\(\left(-3\right)+2.2-1=0\Rightarrow A\in d\)
Thay \(x=5;y=2\) vào PT (d) ta được
\(5+2.2-1=8\ne0\Rightarrow B\notin d\)
b) \(\left(d\right):x+2y-1=0\) có VTPT là \(\overrightarrow{n}=\left(1;2\right)\)
\(\Rightarrow\left(d\right)\) có VTCP là \(\overrightarrow{u}=\left(2;-1\right)\)
PT tham số của (d): \(\left\{{}\begin{matrix}x=-3+2t\\y=2-t\end{matrix}\right.\left(t\in R\right)\)
c) \(d\left(C;\left(d\right)\right)=\dfrac{\left|0+2.2-1\right|}{\sqrt{1^2+2^2}}=\dfrac{3}{\sqrt{5}}=\dfrac{3\sqrt{5}}{5}\)

a: =>x^2-9x-31=9-3x
=>x^2-6x-40=0
=>(x-10)(x+4)=0
=>x=-4 hoặc x=10
b: =>x<=2 và 10x^2+2x-116=16x^2-64x+64
=>x<=2 và -6x^2+66x-180=0
=>\(x\in\varnothing\)
c: =>x^2+x-56<=0
=>(x+8)(x-7)<=0
=>-8<=x<=7


1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25





 giúp em bài này với ạ
giúp em bài này với ạ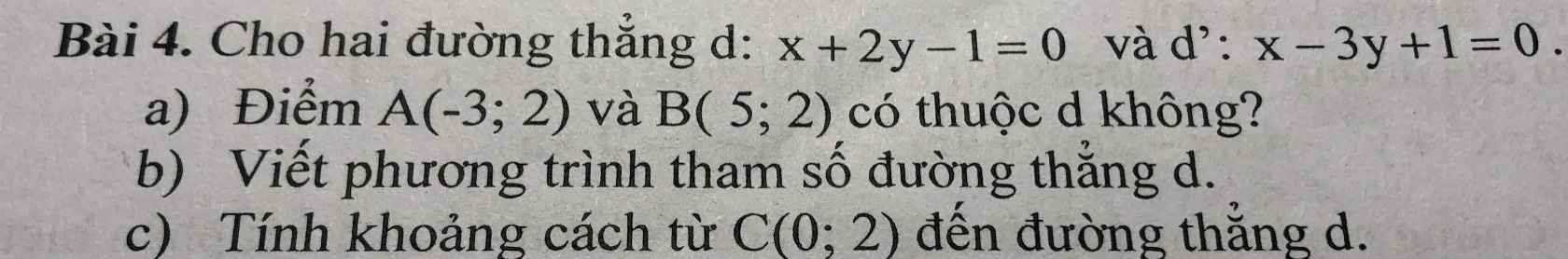
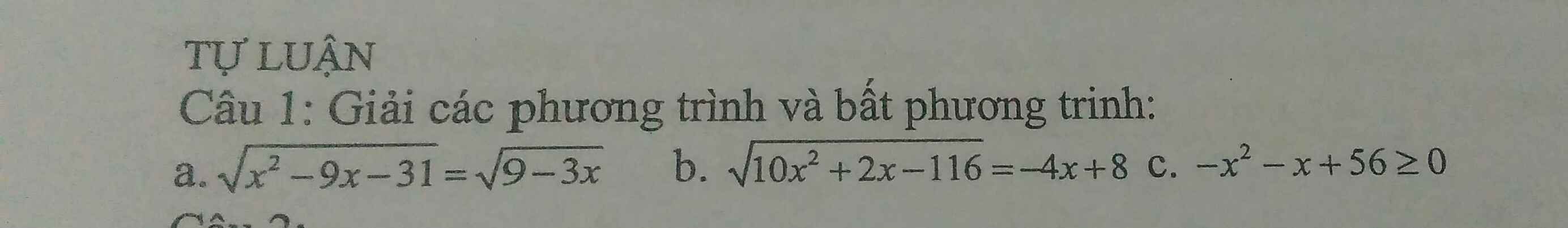




a. Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{AM}=\left(x-1;y+1\right)\)
\(\overrightarrow{AM}=\overrightarrow{a}\Rightarrow\left\{{}\begin{matrix}x-1=3\\y+1=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=4\end{matrix}\right.\)
\(\Rightarrow M\left(4;4\right)\)
b. Do B thuộc Ox nên tọa độ có dạng: \(B\left(x;0\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(x-1;1\right)\)
\(\overrightarrow{AB}\) cùng phương \(\overrightarrow{a}\) khi: \(\dfrac{x-1}{3}=\dfrac{1}{5}\Rightarrow x=\dfrac{8}{5}\)
\(\Rightarrow B\left(\dfrac{8}{5};0\right)\)
c.
\(\overrightarrow{OA}=\left(1;-1\right)\Rightarrow T=1.3+\left(-1\right).5=-2\)
\(\Rightarrow cos\left(\overrightarrow{a},\overrightarrow{OA}\right)=\dfrac{\overrightarrow{a}.\overrightarrow{OA}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{OA}\right|}=\dfrac{-2}{\sqrt{1^2+\left(-1\right)^2}.\sqrt{3^2+5^2}}=-\dfrac{1}{\sqrt{17}}\)