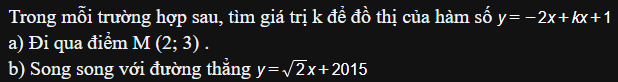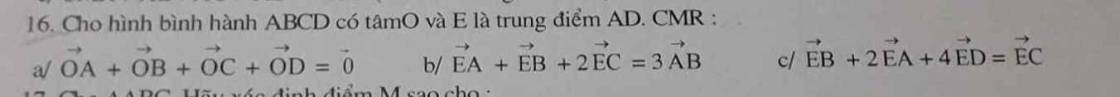Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Delta'=\left(3m\right)^2-m.\left(8m-10\right)=9m^2-8m^2+10m=m^2+10m\)
Để pt có 2 nghiệm phân biệt \(\Delta'>0\Leftrightarrow m^2+10m>0\Leftrightarrow m\left(m+10\right)>0\)
Xét 2 trường hợp:
+) m > 0 và m > -10 => m > 0
+) m < 0 và m < -10 => m < -10
Vậy m > 0 hoặc m < -10 thì pt có 2 nghiệm phân biệt

a.
\(\overline{A}:"\exists x\in R,x^2+x+1\le0"\)
Do mệnh đề A đúng nên \(\overline{A}\) sai
b.
\(\overline{B}:"\exists x\in R,x^2< 0"\)
Do B đúng nên \(\overline{B}\) sai

\(tan\dfrac{\pi}{6}+tan\dfrac{2\pi}{9}+tan\dfrac{5\pi}{18}+tan\dfrac{\pi}{3}\)\(=\left(tan\dfrac{\pi}{6}+tan\dfrac{\pi}{3}\right)+\left(tan\dfrac{2\pi}{9}+tan\dfrac{5\pi}{18}\right)\) (1)
Áp dụng công thức: \(tanx+tan\left(90^o-x\right)=tanx+cotx=\dfrac{1}{sinx.cosx}\)
Ta được:(1) = \(\dfrac{1}{sin\dfrac{\pi}{6}cos\dfrac{\pi}{6}}+\dfrac{1}{sin\dfrac{2\pi}{9}.cos\dfrac{2\pi}{9}}\)
\(=\dfrac{2}{sin\dfrac{\pi}{3}}+\dfrac{3}{sin\dfrac{4\pi}{9}}\)
Em làm tiếp nhé.


a: Thay x=2 và y=3 vào hàm số, ta được:
\(2k+2-4=3\)
\(\Leftrightarrow k=\dfrac{5}{2}\)

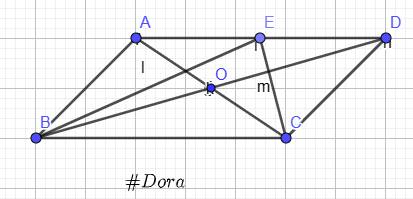
`a)` Vì `O` là trung điểm của `AC;BD`
`=>{(\vec{OA}=-\vec{OC}),(\vec{OB}=-\vec{OD}):}`
Ta có: `\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}`
`=-\vec{OC}-\vec{OD}+\vec{OC}+\vec{OD}=0`
`b)` Vì `E` là trung điểm `AD=>\vec{EA}=-\vec{ED}`
Ta có: `\vec{EA}+\vec{EB}+2\vec{EC}`
`=\vec{EA}+\vec{EA}+\vec{AB}+2\vec{ED}+2\vec{DC}`
`=-2\vec{ED}+\vec{AB}+2\vec{ED}+2\vec{AB}=3\vec{AB}`
`c)` Ta có: `\vec{EB}+2\vec{EA}+4\vec{ED}`
`=\vec{EB}-2\vec{ED}+4\vec{ED}`
`=\vec{EB}+2\vec{ED}`
`=\vec{EA}+\vec{AB}+2\vec{ED}`
`=-\vec{ED}+\vec{AB}+2\vec{ED}`
`=\vec{AB}+\vec{EC}+\vec{CD}` (Mà `\vec{AB}=-\vec{CD}`)
`=\vec{EC}`


 bai nay
bai nay