K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 10 2021
Bài 4:
\(A=2x^2+3x-10x-15-2x^2+6x+x+7=-8\\ B=x^3-y^3-5+2y^3-x^3-y^3=-5\\ C=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6x^2+6=4\)
21 tháng 10 2021
Bài 4:
b: \(B=\left(x-y\right)\left(x^2+xy+y^2\right)+2y^3-5-\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3-y^3+2y^3-5-x^3-y^3\)
=-5
c: \(C=\left(x-1\right)^3-\left(x+1\right)^3-6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6\left(x^2-1\right)\)
\(=-6x^2-2-6x^2+6\)
\(=-12x^2+4\)
2 tháng 10 2021
Câu 5:
a: Ta có: \(A=\left(x-1\right)\left(x-3\right)+11\)
\(=x^2-4x+3+11\)
\(=x^2-4x+4+10\)
\(=\left(x-2\right)^2+10\ge10\forall x\)
Dấu '=' xảy ra khi x=2
b: Ta có: \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)
2 tháng 10 2021
Câu 5:
a) \(A=\left(x-1\right)\left(x-3\right)+11=x^2-4x+3+11\)
\(=x^2-4x+14\)
\(=\left(x^2-4x+4\right)+10=\left(x-2\right)^2+10\ge10\)
\(minA=10\Leftrightarrow x=2\)
b) \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)
9 tháng 12 2021
Bài 2:
b: \(\Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
NN
22 tháng 4 2021
a) Ta có: AB//CD.
=>ABH=BDC (2 góc so le trong).
=> ∆AHB~∆BCD(g.g).
b) ∆ABD có : DB²=AB²+AD²( Định lý Pitago)
=> DB= 15(cm).
Ta có ∆ABH~∆BCD(cmt).
=>AH/BC=AD/BD.
Hay AH=9.12/15=7,2(cm).
c)Ta có ∆AHB~∆BCD cmt.
=> HBA=CBD. (1)
Ta lại có : CBD= ADH (AB//CD).(2)
Từ 1 và 2 => HAB=ADH.
=>∆DHA~∆AHB(g.g).
S∆DHA/S∆AHB=(AD/AB)²=9/16
d) từ câu (a) và (b) => ∆BCD~∆DHA.
Cm ∆DHA~∆MDA(g.g)
Từ đó suy ra ∆BDC~∆MDA.
Sau đó cm ∆BCD~∆ADC(g.g).
=> ∆MDA~∆ADC(g.g).
=>Ad/DC=DM/DC.
=>Đpcm.
18 tháng 1 2022
c, Vì ME⊥AC và BA⊥AC
⇒ ME// AB (1)
Mà M là trung điểm của BC
⇒ E là trung điểm của AC
⇒ ME là đường TB của ΔABC
\(\Rightarrow ME=\dfrac{1}{2}AB\)
Chứng minh tương tự ta có: D là trung điểm của AB
⇒ DA=DB
⇒ ME=DA=DB (2)
Từ (1)(2) ⇒ BDEM là hình bình hành
18 tháng 1 2022
Ta có:
AM=1/2MB(GT) ➪AM=MB
Xét tam giác AMB, ta có:
AM=MB ( CMT)
➪ Tam giác AMB là tam giác cân mà MD lại là đường cao của tam giác AMB( do MD┷ AB (GT))
➪ MD vừa là đường cao vừa là đường cao vừa là đường trung tuyến của tam giác AMB (T/C)
➪ DA=DB mà EM=AD ( do EMDA là hình chữ nhật (CM ở b))
➪ EM=DB (1)
Ta có:
ED=MA( do do EMDA là hình chữ nhật (CM ở b))
mà MA=MB (CMT)
➪MB=ED(2)
Từ (1) và (2)
➪ EMBD là hình bình hành (DHNB)
NT
1
2 tháng 7 2023
4:
a: Xét ΔEFA và ΔAMC có
góc EFA=góc AMC(=góc EIM)
góc EAF=góc ACM
=>ΔEFA đồng dạng với ΔAMC
=>EF/AM=EA/AC
=>EF*AC=AM*EA
b: ΔEFA đồng dạng với ΔAMC
=>S EFA/S AMC=(EF/AM)^2=1/9
=>S EFA=1/9*S AMC
mà S AMC=1/2*S ABC
nên S EFA=1/9*1/2*S ABC=1/18*S ABC
BC
0
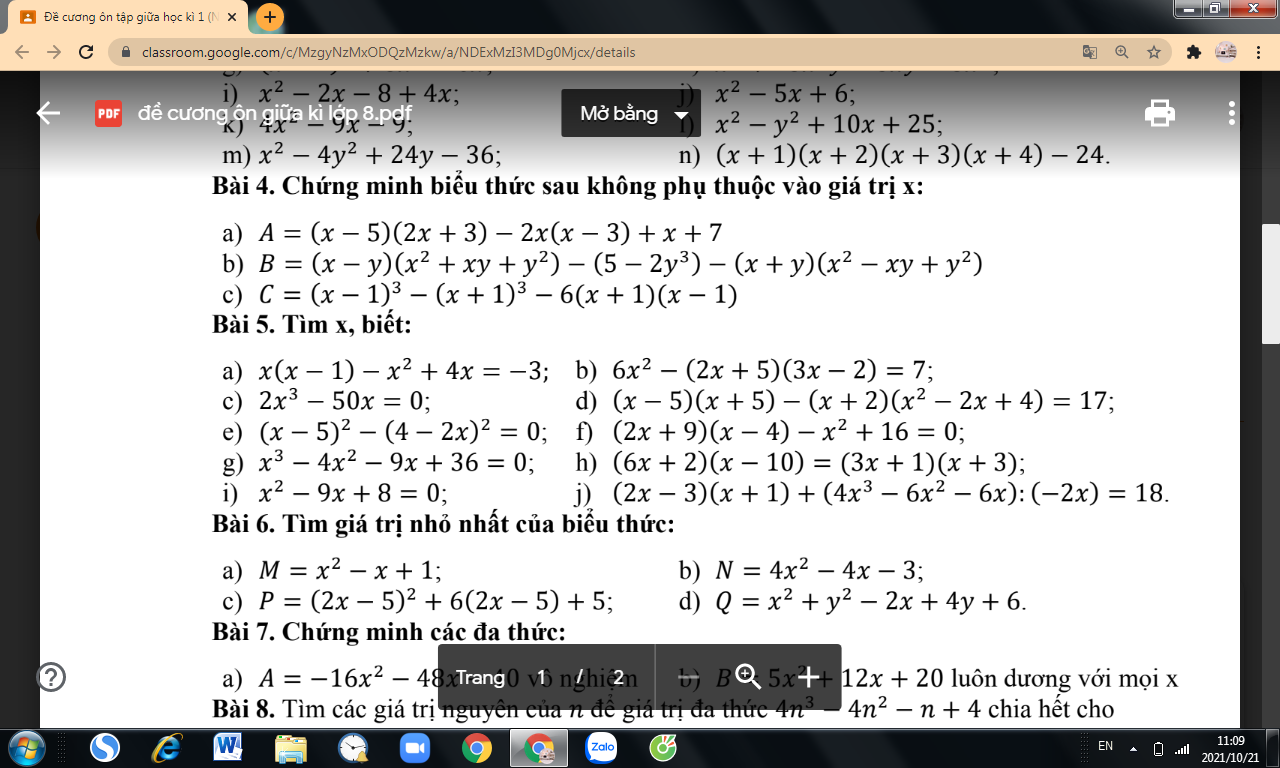
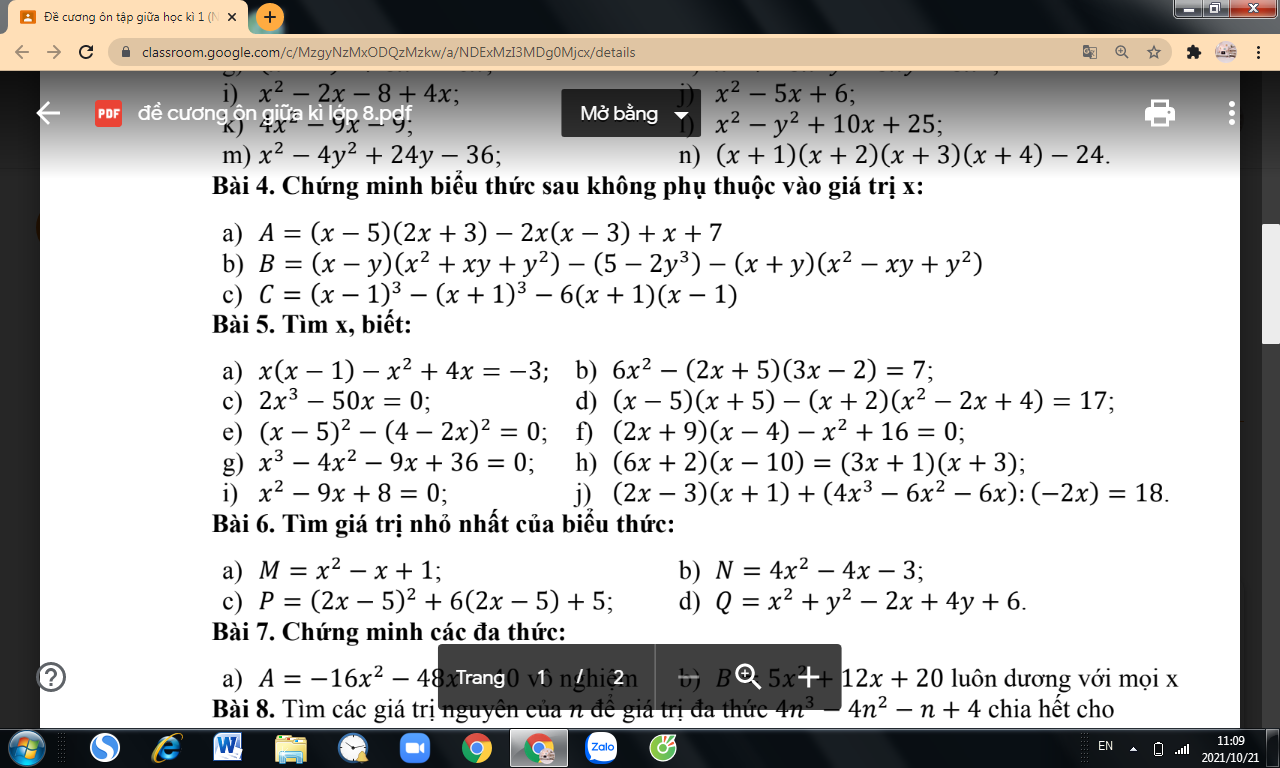
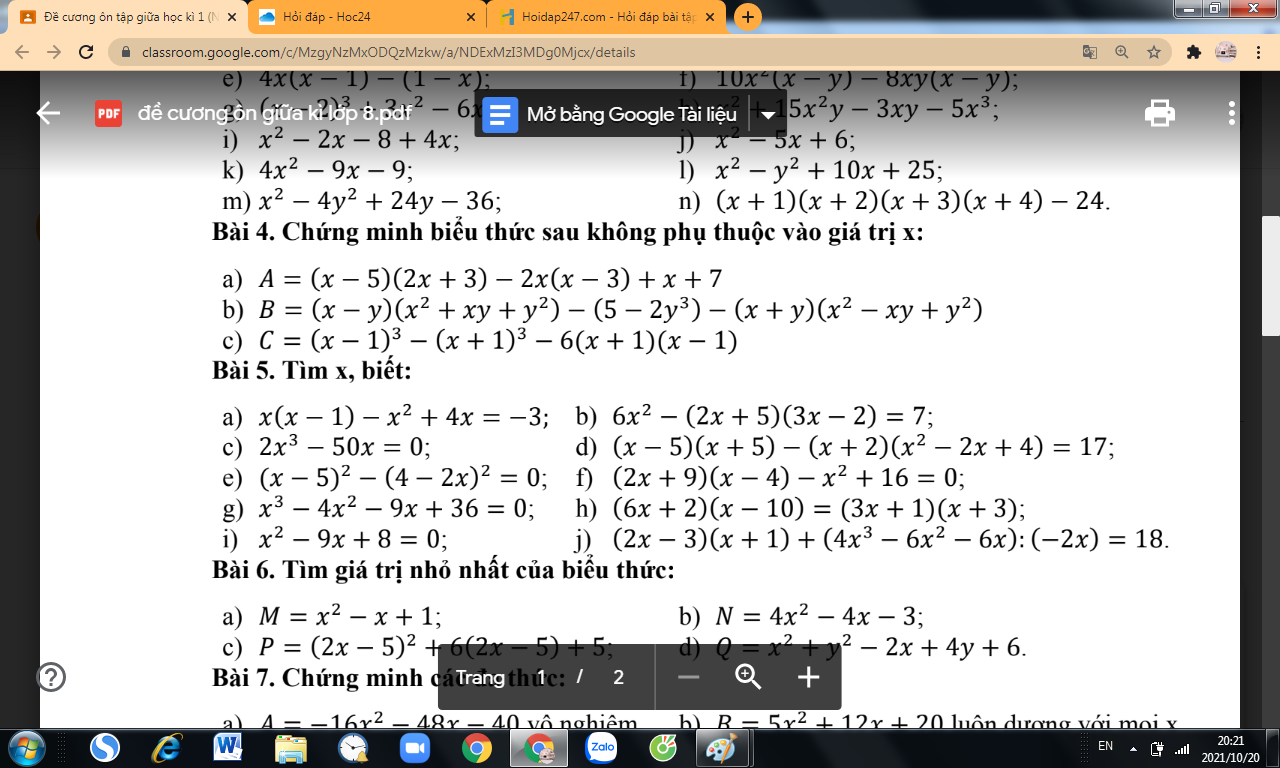
Lời giải:
a. Tứ giác $ENHK$ có $\widehat{H}=\widehat{K}=\widehat{N}=90^0$ nên $ENHK$ là hình chữ nhật.
$\Rightarrow EN=HK(1)$ (tính chất hình chữ nhật)
b.
Xét tam giác $BHA$ và $ANE$ có:
$\widehat{BHA}=\widehat{ANE}=90^0$
$\widehat{HBA}=90^0-\widehat{BAH}=\widehat{NAE}$
$\Rightarrow \triangle BHA\sim \triangle ANE$ (g.g)
$\Rightarrow \frac{HA}{NE}=\frac{BA}{AE}=1$
$\Rightarrow HA=NE(2)$
Từ $(1); (2)\Rightarrow HA=HK$
c. Gọi $M$ là giao điểm $BI$ và $AH$
Vì $BAE$ là tam giác cân tại $A$ nên đường trung tuyến $AI$ đồng thời là đường cao.
$\Rightarrow AI\perp BE$
Xét tam giác $BMH$ và $AMI$ có:
$\widehat{BHM}=\widehat{AIM}=90^0$
$\widehat{BMH}=\widehat{AMI}$ (đối đỉnh)
$\Rightarrow \triangle BMH\sim \triangle AMI$ (g.g)
$\Rightarrow \frac{BM}{MH}=\frac{AM}{MI}$
Xét tam giác $BMA$ và $HMI$ có:
$\widehat{BMA}=\widehat{HMI}$ (đối đỉnh)
$\frac{BM}{HM}=\frac{MA}{MI}$ (cmt)
$\Rightarrow \triangle BMA\sim \triangle HMI$ (g.g)
$\Rightarrow \widehat{MBA}=\widehat{MHI}$
$\Rightarrow \widehat{EBA}=\widehat{AHI}$
Mà $\widehat{EBA}=45^0$ (do $BAE$ vuông cân tại $A$)
$\Rightarrow \widehat{AHI}=45^0$
Hình vẽ: