K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 3 2022
Đăng tách ra bạn nhé
Vì AD là pg \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{5}{4}=\dfrac{3}{DC}\Rightarrow DC=\dfrac{12}{5}cm\)
BC = DC + DB = 12/5 + 3 = 27/5 cm
chọn B
31 tháng 10 2021
3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
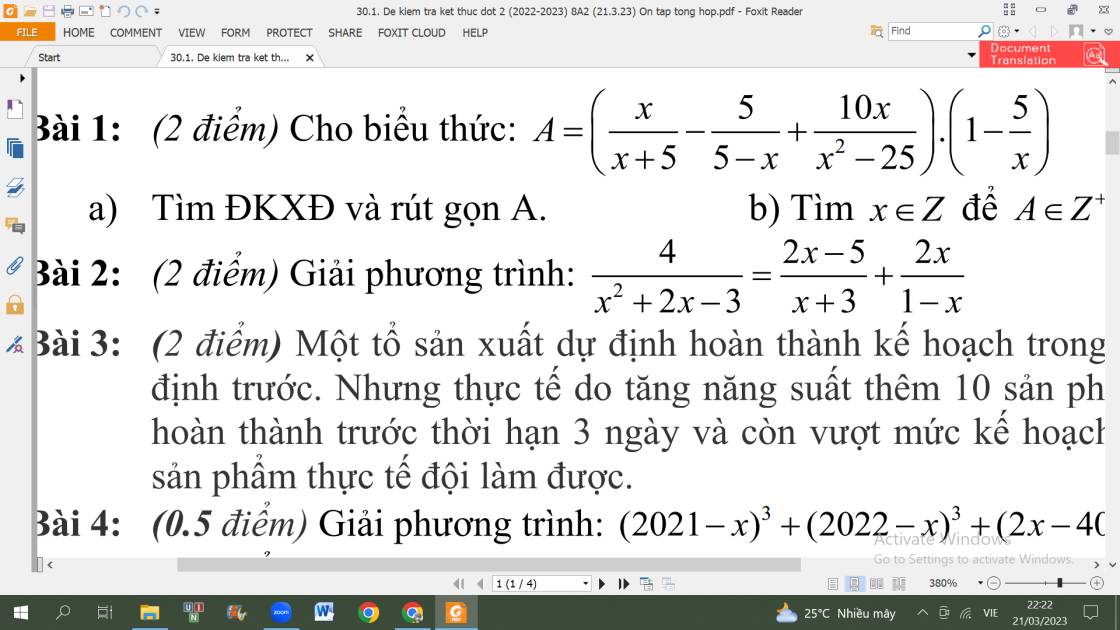
1.
a. ĐKXĐ: \(x\ne\left\{0;-5;5\right\}\)
\(A=\left(\dfrac{x}{x+5}+\dfrac{5}{x-5}+\dfrac{10x}{x^2-25}\right).\left(1-\dfrac{5}{x}\right)\)
\(=\left(\dfrac{x\left(x-5\right)}{\left(x-5\right)\left(x+5\right)}+\dfrac{5\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}+\dfrac{10x}{\left(x-5\right)\left(x+5\right)}\right).\left(\dfrac{x-5}{x}\right)\)
\(=\left(\dfrac{x^2-5x+5x+25+10x}{\left(x-5\right)\left(x+5\right)}\right)\left(\dfrac{x-5}{x}\right)\)
\(=\left(\dfrac{x^2+10x+25}{\left(x-5\right)\left(x+5\right)}\right)\left(\dfrac{x-5}{x}\right)\)
\(=\dfrac{\left(x+5\right)^2\left(x-5\right)}{\left(x-5\right)\left(x+5\right).x}=\dfrac{x+5}{x}\)
b.
\(A=\dfrac{x+5}{x}=1+\dfrac{5}{x}\)
\(A\in Z\Rightarrow\dfrac{5}{x}\in Z\Rightarrow5⋮x\)
\(\Rightarrow x=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\)
Thay vào ta được \(A=\left\{0;-4;6;2\right\}\)
Do A nguyên dương nên loại \(A=\left\{0;-4\right\}\) tương ứng \(x=\left\{-5;-1\right\}\)
Vậy \(x=\left\{1;5\right\}\)
21 tháng 3 2023
2:
=>4=(2x-5)(x-1)-2x(x+3)
=>2x^2-2x-5x+5-2x^2-6x=4
=>-13x+5=4
=>-13x=-1
=>x=1/13
5 tháng 1 2022
Bài 2:
a: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(P=\dfrac{x}{3\left(x-1\right)}-\dfrac{x^2-1}{3\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+x-x^2+1}{3\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{3\left(x-1\right)\left(x+1\right)}=\dfrac{1}{3x-3}\)
b: Để P=2 thì 3x-3=1/2
=>3x=7/2
=>x=7/6
c: Vì x=1 không thỏa mãn ĐKXĐ nên khi x=1 thì P không có giá trị
CL
Giải bài 4 và bài 5 và bài 6 nhớ giải chi tiết giúp mik
0
T
1 tháng 10 2019
\(x^3+9x^2+27x+26=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+7x+13\right)=0\Rightarrow x=-2\)
1 tháng 10 2019
\(x^3+9x^2+27x+26=0\)
\(\Leftrightarrow x^3+9x^2+27x+27=1\)
\(\Leftrightarrow\left(x+3\right)^3=1^3\)
\(\Leftrightarrow x+3=1\Leftrightarrow x=-2\)
TC
1
6 tháng 5 2017
1,2 - ( x - 0,8 ) = -2( 0,9 + x )
<=> 1,2 - x + 0,8 = -1,8 - 2x
<=> 1,2 + 0,8 + 1,8 = -2x + x
<=> 3,8 = -x
<=> -3 ,8 = x
Nghiệm của phương trình là <-3,8>
NT
1
AH
Akai Haruma
Giáo viên
23 tháng 2 2021
Những bài hình học thì bạn nên chia nhỏ ra để được hỗ trợ tốt hơn, để như thế này khiến người đọc rất "nản"
1
a
\(=x\left(x^2+xy\right)-z\left(x^2+xy\right)\\ =\left(x-z\right)\left(x^2+xy\right)\)
b
\(=12\left(xy-xz\right)+3x\left(xy-xz\right)\\ =\left(12+3x\right)\left(xy-xz\right)\\ =x\left(12+3x\right)\left(y-z\right)\)
c
\(=\dfrac{1}{2}\left(x^4+2x^2y^2+y^4\right)-\dfrac{1}{2}.4x^2y^2\\ =\dfrac{1}{2}\left(x^4+2x^2y^2+y^4-4x^2y^2\right)\\ =\dfrac{1}{2}\left(x^4-2x^2y^2+y^4\right)\\ =\dfrac{1}{2}\left(x^2-y^2\right)^2\\ =\dfrac{1}{2}\left(x^2-y^2\right)\left(x^2-y^2\right)\\ =\dfrac{1}{2}\left(x-y\right)\left(x+y\right)\left(x-y\right)\left(x+y\right)\)
d
\(=2\left(x-y\right)^2-2.\left(5xy\right)^2\\ =2\left[\left(x-y\right)^2-\left(5xy\right)^2\right]\\ =2\left(x-y-5xy\right)\left(x-y+5xy\right)\)
2
\(5x^2z-10xyz+5y^2z\\ =5x^2z-5xyz-5xyz+5y^2z\\ =\left(5x^2z-5xyz\right)-\left(5xyz-5y^2z\right)\\ =5xz\left(x-y\right)-5yz\left(x-y\right)\\ =\left(5xz-5yz\right)\left(x-y\right)\\ =5z\left(x-y\right)\left(x-y\right)\\=5z\left(x-y\right)^2\)
Thế \(x=124;y=24;z=2\) vào biểu thức được:
\(5.2\left(124-24\right)^2=10.\left(100\right)^2=10.10000=100000\)