
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ta có: ADHE là hình chữ nhật
=>AH=DE(1)
Ta có: ΔAHM vuông tại H
=>AH<AM(2)
Từ (1) và (2) suy ra DE<AM
c: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nênMA=MC
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
Ta có: AEHD là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{B}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{B}\)
Ta có: \(\widehat{AED}+\widehat{MAC}\)
\(=\widehat{B}+\widehat{C}=90^0\)
=>DE\(\perp\)AM
d:Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường trung tuyến ứng với cạnh BC
=>H trùng với M
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc DAE
Xét hình chữ nhật ADHE có AH là phân giác của góc DAE
nên ADHE là hình vuông
=>Chu vi là \(C=3\cdot4=12cm\) và diện tích \(S=3^2=9\left(cm^2\right)\)

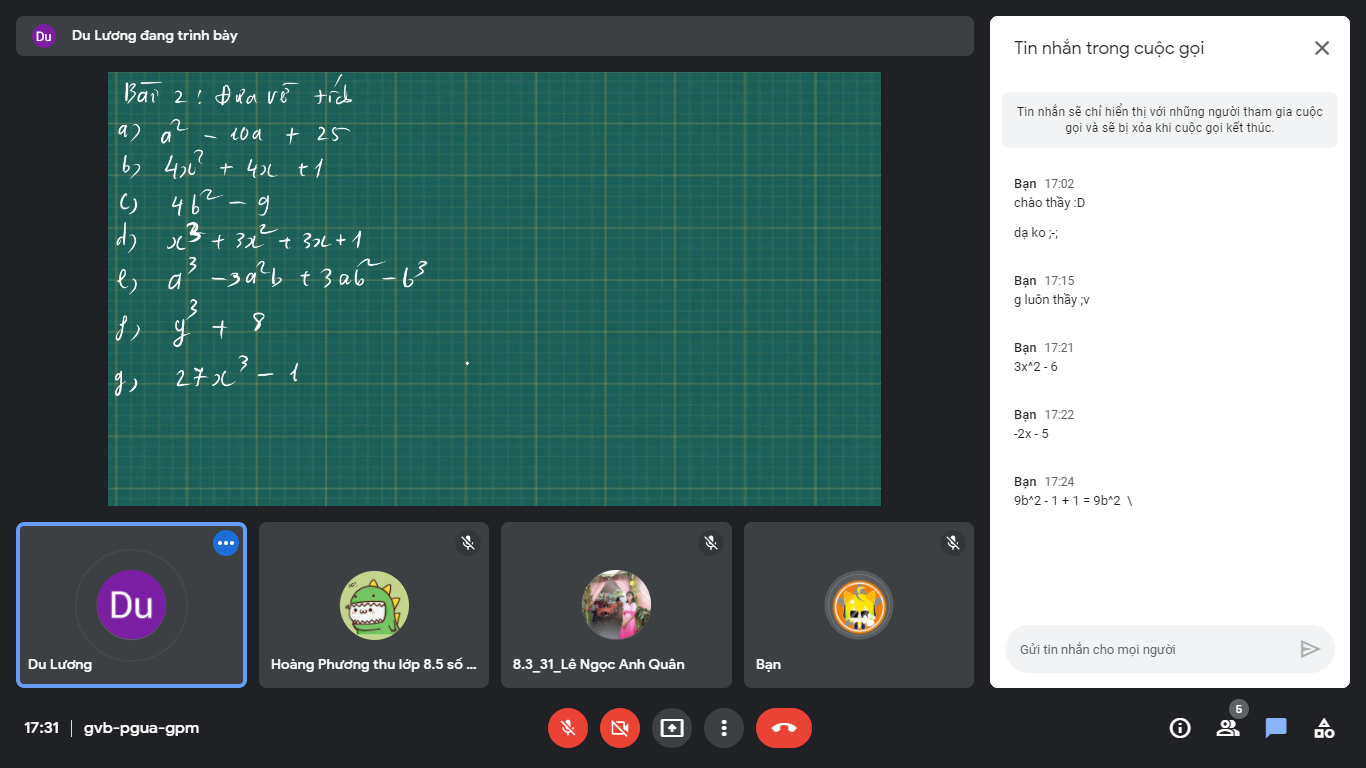
\(a,a^2-10a+25=\left(a-5\right)^2\\ b,4x^2+4x+1=\left(2x+1\right)^2\\ c,4x^2-9=\left(2x-3\right)\left(2x+3\right)\\ d,x^3+3x^2+3x+1=\left(x+1\right)^3\\ e,a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\\ f,y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\\ g,27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)
\(a^2-10x+25=\left(a-5\right)^2\)
b/ \(4x^2+4x+1=\left(2x+1\right)^2\)
c/ \(4b^2-9=\left(2b-3\right)\left(2b+3\right)\)
d/ \(x^3+3x^2+3x+1=\left(x+1\right)^3\)
e/ \(a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\)
f/ \(y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\)
g/ \(27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)

a) \(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\left(Đk:x\ne3\right)\)
\(A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}=x-y\)
b) \(\dfrac{5x}{x+1}=\dfrac{Ax\left(x-1\right)}{\left(1-x\right)\left(x+1\right)}\left(Đk:x\ne\pm1\right)\)
\(A=\dfrac{5x\left(1-x\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-5\)
c) \(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\left(Đk:x\ne-3;A\ne0\right)\)
\(A=\dfrac{\left(4x^2-5x+1\right)\left(x+3\right)}{4x-1}=\dfrac{\left(x-1\right)\left(4x-1\right)\left(x+3\right)}{4x-1}\)
\(=\left(x-1\right)\left(x+3\right)=x^2+2x-3\)


a) \(A=x^4+4x+7=\left(x^2+4x+4\right)+3=\left(x+2\right)^2+3\ge3\)
\(minA=3\Leftrightarrow x=-2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxC=7\Leftrightarrow x=2\)
d) \(D=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxD=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)

a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)


\(\dfrac{x-3}{3}=4-\dfrac{1-2x}{5}\)
=>5(x-3)=60-3(1-2x)
=>5x-15=60-3+6x
=>5x-15=6x+57
=>6x+57=5x-15
hay x=-72(nhận)


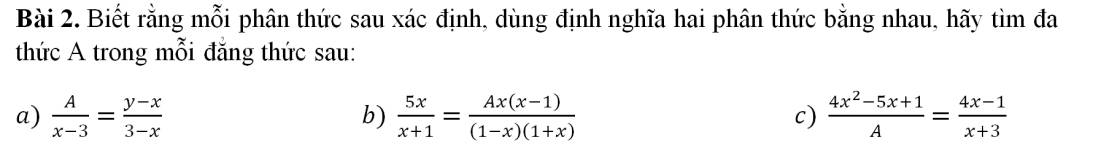 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 

 giúp em bài này vs ạ em cảm ơn trc ạ
giúp em bài này vs ạ em cảm ơn trc ạ

\(\left\{{}\begin{matrix}a,x^2+2x+1=\left(x+1\right)^2\\b,\left(3x+2y\right)^2=9x^2+12xy+4y^2\\c,36+x^2-12x=\left(x-6\right)^2\\d,\left(2x+5y\right)^2=4x^2+20xy+25y^2\end{matrix}\right.\)