
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: =>(x+5)(4-x)=0
=>x=4 hoặc x=-5
b: =>2x(2x-1)=0
=>x=0 hoặc x=1/2
c: =>2x(x^2+1)+x^2+1=0
=>(x^2+1)(2x+1)=0
=>2x+1=0
=>x=-1/2
d: Δ=(-3)^2-4*1*4=9-16=-7<0
=>PTVN


\(P=\dfrac{4x}{x-2}=\dfrac{4\left(x-2\right)+8}{x-2}=4+\dfrac{8}{x-2}\in Z\)
\(\Rightarrow\left(x-2\right)\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
\(\Rightarrow x\in\left\{-6;-2;0;1;3;4;6;10\right\}\)

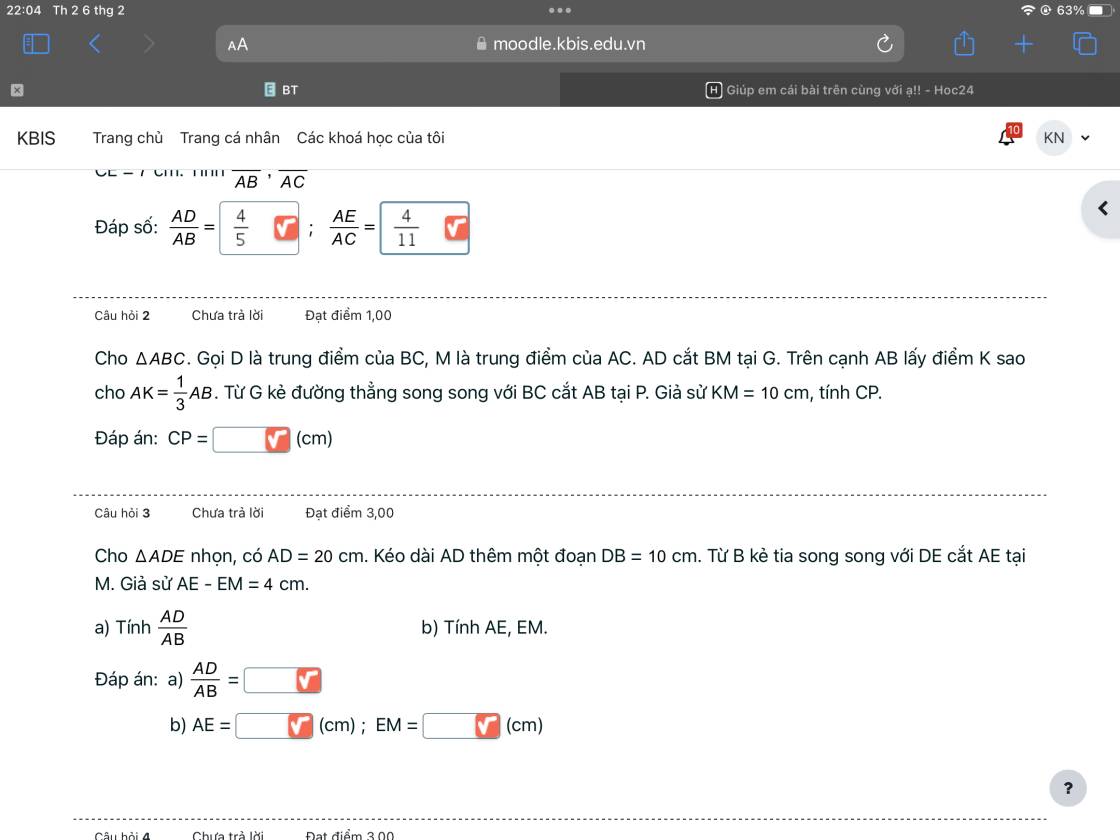
Xét ΔADB có PQ//BD
nên AQ/AD=AP/AB=2/3
=>AP=2/3AB=2AK
=>K là trung điểm của AP
Xét ΔAPC có
K,M lần lượt là trung điểm của AP,AC
nên KM là đường trung bình
=>KM//PC và KM=PC/2
=>PC=20cm

Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)

Ta có:
AE vuông góc BD
CF vuông góc BD
=> AE//CF(1)
Xét 2 tam giác vuông AED và CFB có:
AD=BC
góc ADB = góc CBF ( 2 góc slt)
=> tam giác AED = tam giác CFB (ch-gn)
=> AE= CF (2)
Từ (1) và (2) => AECF là hbh ( đpcm)



6:
a: Xét ΔCDM và ΔBAM có
MC=MB
góc CMD=góc BMA
MD=MA
=>ΔCDM=ΔBAM
b: ΔCDM=ΔBAM
=>góc CDM=góc BAM
=>CD//AB
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD và AC=BD và AB=DC
c: Xét ΔABC có AB>AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB>HC
Xét ΔECB có HB>HC
mà HB,HC lần lượt là hình chiếu của EB,EC trên BC
nên EB>EC







\(B=\left(\frac{x-2}{2x-2}-\frac{3}{2-2x}-\frac{x+3}{2x+2}\right):\left(1-\frac{x-3}{x+1}\right)\) \(ĐKXĐ:x\ne\pm1\)
\(B=\left(\frac{\left(x-2\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}+\frac{3\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}-\frac{\left(x+3\right)\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\right)\)\(:\left(\frac{x+1-x+3}{x+1}\right)\)
\(B=\left(\frac{x^2-x-2+3x+3-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right):\left(\frac{4}{x+1}\right)\)
\(B=\left(\frac{4}{2\left(x-1\right)\left(x+1\right)}\right):\left(\frac{4}{x+1}\right)\)
\(B=\frac{4}{2\left(x-1\right)\left(x+1\right)}.\frac{x+1}{4}=\frac{1}{2\left(x-1\right)}\)