
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b: Sửa đề: AO vuông góc BI
Gọi M là trung điểm của IC
Xét ΔIHC có IO/IH=IM/IC
nên OM//HC và OM=1/2HC
=>OM vuông góc AH
Xet ΔAHM có
MO,HI là đường cao
MO cắt HI tại O
=>O là trực tâm
=>AO vuông góc HM
=>AO vuông góc BI

Ta có:
HA1/AA1 = S(HBC)/S(ABC)
HB1/BB1 = S(HAC)/S(ABC)
HC1/CC1 = S(HAB)/S(ABC)
cộng theo vế được:
HA1/AA1 + HB1/BB1 + HC1/CC1 = S(HBC)/S(ABC) + S(HAC)/S(ABC) + S(HAB)/S(ABC)
= S(ABC) / S(ABC = 1
Ap dụng bất đẳng thức:
(a+b+c)(1/a+1/b+1/c) ≥ 9 dấu = xảy ra khi a =b =c
Ta có:
(HA1/AA1 + HB1/BB1 + HC1/CC1)(AA1/HA1 + BB1/HB1 + CC1/HC1) ≥ 9
mà: HA1/AA1 + HB1/BB1 + HC1/CC1 = 1
=> AA1/HA1 + BB1/HB1 + CC1/HC1 ≥ 9
<=> (AH + HA1)/HA1 + (BH + HB1)/HB1 + (CH + HC1)/HC1 ≥ 9
<=> AH/HA1 + 1 + BH/HB1 + 1 + CH/HC1 + 1 ≥ 9
=> AH/HA1 + BH/HB1 + CH/HC1 ≥ 6
k cho mk nhé.Chúc bạn học giỏi

\(a,\) Vì M,N là trung điểm AB,BC nên MN là đtb \(\Delta ABC\)
Do đó \(MN//BC\Rightarrow MN//KC\) và \(MN=\dfrac{1}{2}BC=KC\) (K là trung điểm)
Vậy MNCK là hình bình hành
\(b,\) Vì MN là đtb nên \(AC=2MN=10(cm)\)
Áp dụng Pytago: \(HC^2=AC^2-AH^2=6(cm)\)
Vậy \(S_{ACH}=\dfrac{1}{2}AH.HC=\dfrac{1}{2}.6.8=24(cm^2)\)
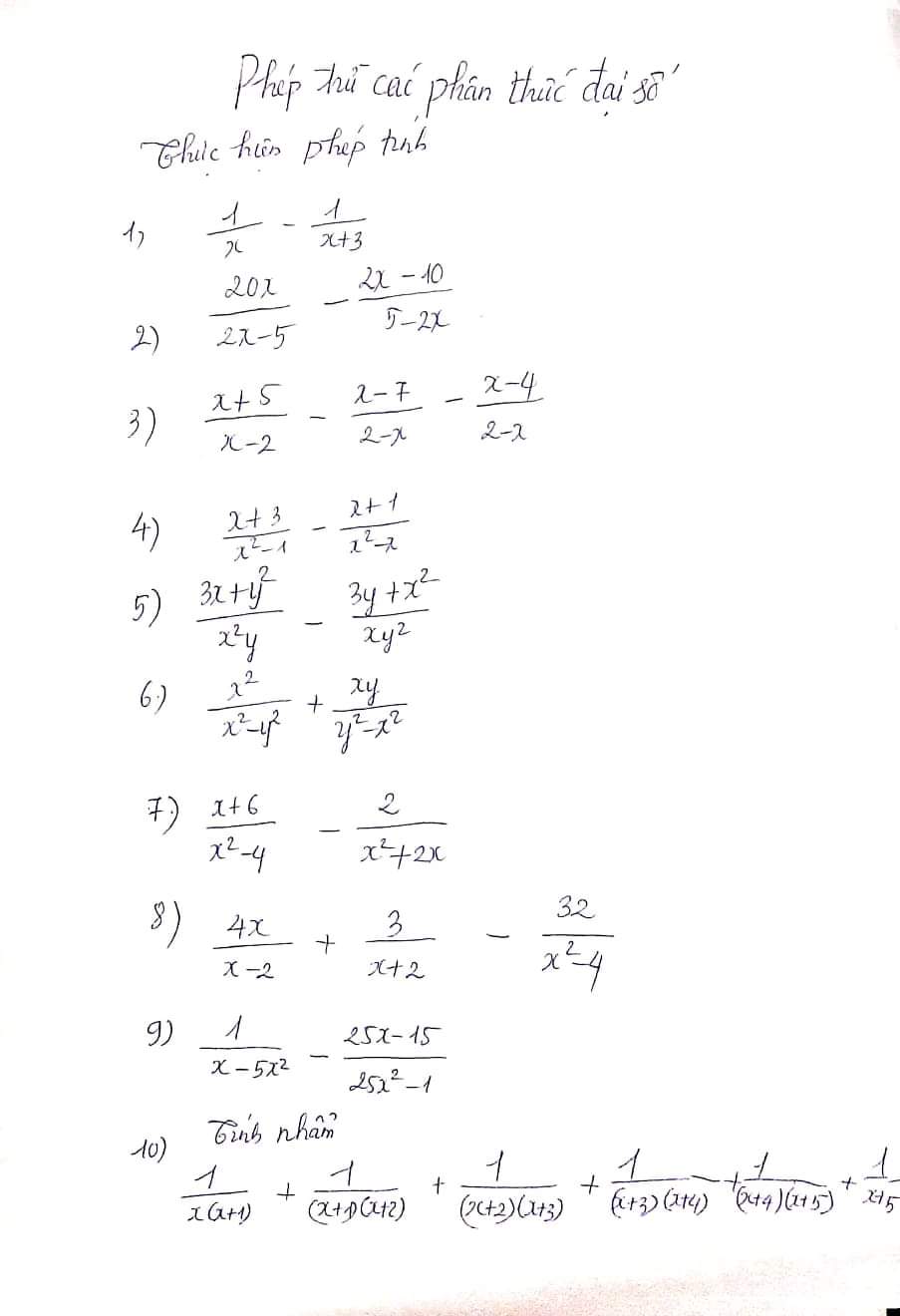
 giúp e với ah
giúp e với ah
\(1,=\dfrac{x+3-x}{x\left(x+3\right)}=\dfrac{3}{x\left(x+3\right)}\\ 2,=\dfrac{20x+2x-10}{2x-5}=\dfrac{22x-10}{2x-5}\\ 3,=\dfrac{x+5+x-7+x-4}{x-2}=\dfrac{3\left(x-2\right)}{x-2}=3\\ 4,=\dfrac{x^2+3x-x^2-2x-1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x\left(x+1\right)}\\ 5,=\dfrac{3xy+y^3-3xy-x^3}{x^2y^2}=\dfrac{y^3-x^3}{x^2y^2}\\ 6,=\dfrac{x^2-xy}{\left(x-y\right)\left(x+y\right)}=\dfrac{x\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{x}{x+y}\)
\(7,=\dfrac{x^2+6x-2x+4}{x\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)^2}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x+2}{x\left(x-2\right)}\\ 8,=\dfrac{4x^2+8x+3x-6-32}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x^2+11x-38}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-2\right)\left(4x+19\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x+19}{x+2}\\ 9,=\dfrac{-5x-1-25x^2+15x}{x\left(5x-1\right)\left(5x+1\right)}=\dfrac{-\left(5x-1\right)^2}{x\left(5x-1\right)\left(5x+1\right)}=\dfrac{1-5x}{x\left(5x+1\right)}\\ 10,=\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+...+\dfrac{1}{x-4}-\dfrac{1}{x+5}+\dfrac{1}{x+5}=\dfrac{1}{x}\)
Em camon ă